LIGA ZADANIOWA UMK W TORUNIU 2004/2005
ZADANIA ĆWICZENIOWE DO ETAPU I
DLA KLAS II GIMNAZJUM
Zadanie 2
Wewnątrz czworokąta wypukłego znaleźć punkt, dla którego suma odległości od wierzchołków tego czworokąta jest najmniejsza.Rozwiązanie
Narysujmy sobie dowolny czworokąt ABCD i obierzmy dwa punkty - X na przekątnej oraz Y gdziekolwiek(nie na przekątnej!). Połączmy te punkty z wierzchołkami B i D tak jak na rysunku.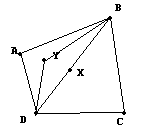 Z nierówności trójkąta wynika, że odcinek YD + YB > XD + XB(czyli mniejszy od przekątnej DB). Dlatego też aby suma odległości od wierzchołków B i D była najmniejsza, to punkt X musi znajdować się na przekątnej DB. Podobnie będzie w przypadku najmniejszej sumy odległości do punktów A i C. X będzie musiał się znajdować na przekątnej AC. Jeżeli X musi być na obu przekątnych,to znaczy, iż X jest punktem przecięcia się przekątnych.
Z nierówności trójkąta wynika, że odcinek YD + YB > XD + XB(czyli mniejszy od przekątnej DB). Dlatego też aby suma odległości od wierzchołków B i D była najmniejsza, to punkt X musi znajdować się na przekątnej DB. Podobnie będzie w przypadku najmniejszej sumy odległości do punktów A i C. X będzie musiał się znajdować na przekątnej AC. Jeżeli X musi być na obu przekątnych,to znaczy, iż X jest punktem przecięcia się przekątnych.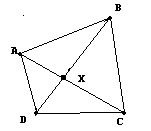
Odp: Tym punktem jest miejsce przecięcia się przekątnych.
Leszek Tatara