LIGA ZADANIOWA UMK W TORUNIU 2004/2005
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS VI SZKÓŁ PODSTAWOWYCH

Zadanie 15

Na prostej obrano w kolejności punkty A, B, C, D, E, F. Jakie są odległości między kolejnymi punktami jeśli wiadomo, że |AF| = 53 cm, |AB| = 2|EF|, |AB| > |BC| > |CD| > |DE| > |EF| i odległości te wyrażają się całkowitymi liczbami centymetrów.

Rozwiązanie:

Oznaczmy długości tych odcinków następująco: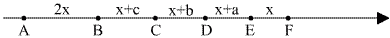

Porównajmy teraz jakie wartości minimalnie i maksymalnie mogą przyjmować długości tych odcinków:

Odcinek Minimum Długość Maksimum
|EF| x x x
|DE| x + 1 x + a x + (x-3)
|CD| x + 2 x + b x + (x-2)
|BC| x + 3 x + c x + (x-1)
|AB| x + x x + x x + x
W sumie:
|AF| 6x + 6 6x + a + b + c = 53 9x - 6

Stąd mamy:

6x + 6 ≤ 53 oraz 9x - 6 ≥ 53
6x ≤ 47   9x ≥ 59
Liczba x ma być całkowita, więc:
x ≤ 7   x ≥ 7

Jedyną liczbą spełniającą oba warunki jest 7, więc

x = 7

Następnie:

6x + a + b + c = 53

6×7 + a + b + c = 53

42 + a + b + c = 53

a + b + c = 11

Przy tym: x + c < 2x, tzn. 7 + c < 14, więc

c < 7

Za a, b, c mozemy podstawić liczby: Mamy wobec tego trzy rozwiązania:

Odcinek I rozwiązanie II rozwiazanie III rozwiązanie
|EF| = x 7 7 7
|DE| = x + a 8 9 9
|CD| = x + b 11 10 11
|BC|= x + c 13 13 12
|AB| = 2x 14 14 14
W sumie:
|AF| 53 53 53

Leszek Tatara