Liga Zadaniowa UMK w Toruniu

Zadanie 4

Ile jest biletów z numerami od 000001 do 999999, w których są dwie cyfry stojące obok siebie i różniące się o 5?

Rozwiązanie

Najpierw policzmy ile jest wszystkich numerów w zbiorze.
{000000,000001,000002...,999999}
Jeśli rozmieścimy te numery tak jak na tym rysunku, to łatwo zobaczyć, że jest ich 10⁶ gdyż pierwszą cyfrę mp żemy wybrać na 10 sposobów. Na każdy taki wybór przypada 10 mozliwości ustawienia cyfry na drugim miejscu. To już daje 100 możliwości, i tak dalej.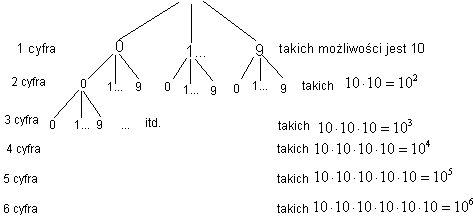

Czyli wszystkich numerów od 000001 do 999999 jest 10⁶-1 (bo musimy odjąć 000000).
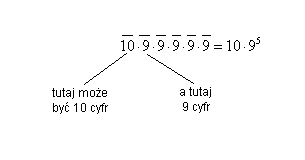
A teraz policzmy ile jest numerów od 000000 do 999999, które nie spełniają warunków zadania.

Pierwsza cyfra może być dowolna od 0 do 9.

Druga cyfra zależy od pierwszej (jeśli na pierwszym miejscu jest 0, to na drugim miejscu nie może być 5, jeśli na pierwszym miejscu jest 1, to na drugim miejscu nie może być 6 i tak dalej, ... jeśli na pierwszym miejscu jest 9, to na drugim miejscu nie może być 4. Zatem drugą cyfrę możemy wstawić tylko na 9 sposobów.

Trzecia cyfra zależy od drugiej i też można ją wstawić na 9 sposobów.

I tak do końca.
Nie zapominajmy jednak o tym, że musimy odjąć 000000. Więc odpowiedź brzmi: 10·9⁵-1.
Teraz wystarczy tylko od liczby biletów odjąć liczbę biletów, które nie spełniają warunków zadania.
(10⁶-1)-(10·9⁵-1)=10⁶-1-10·9⁵+1=10⁶-10·9⁵=409510

Odpowiedź

Jest 409510 biletów, które spełniają warunki zadania.

Agnieszka Biegun