Najpierw obliczmy długość średnicy koła, oznaczmy ją jako c:
c2 = a2 + b2
c2 = 182 + 242
c2 = 324 + 576
c = 30
f jest połową c, a więc f = 15
d = e i jest połową f, a więc d = e = 7,5
LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM
Zadanie 4
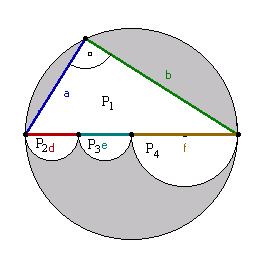
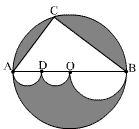 Średnica AB dzieli koło o środku w punkcie O na dwie części. Trójkąt prostokątny ABC ma przyprostokątne długości 18 cm i 24 cm. Punkt D będzie środkiem odcinka AO. Na odcinkach AD, DO i OB zbudowano jako na średnicach półkoła tak, jak to widać na rysunku. Oblicz pole i obwód szarego obszaru.
Średnica AB dzieli koło o środku w punkcie O na dwie części. Trójkąt prostokątny ABC ma przyprostokątne długości 18 cm i 24 cm. Punkt D będzie środkiem odcinka AO. Na odcinkach AD, DO i OB zbudowano jako na średnicach półkoła tak, jak to widać na rysunku. Oblicz pole i obwód szarego obszaru.
Rozwiązanie
 |
Najpierw obliczmy długość średnicy koła, oznaczmy ją jako c: f jest połową c, a więc f = 15 d = e i jest połową f, a więc d = e = 7,5 |
Teraz policzmy pole koła:
P = pr2 = 225p
P2=½ (p7,52) = ½ (56 ¼ p) = 28 1/8 p
P3 = P4 i możemy zauważyć, że przez to, gdy je dodamy otzrymamy jedno koło, więc:
P3 + P4 = p (3,752) = 14 1/16 p
P1 = ½ (24.18) = 216
A więc pole zacieniowanego obszaru wynosi:
225p - 28 1/8 p - 14 1/16 p - 216 = 182 13/16 p - 216
Odpowiedź
Pole zacieniowanego obszaru wynosi: 225p - 28 1/8 p - 14 1/16 p - 216 = 182 13/16 p - 216, a obwód: 30p + 7,5p + 7,5p + 18 + 24 = 45p + 42Autor: Agnieszka Biegun