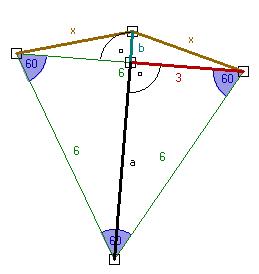
Aby wyglądało to przejrzyściej przerysujmy sam trójkąt (wraz z dwoma bokami dwunastokąta):
LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM
Zadanie 4
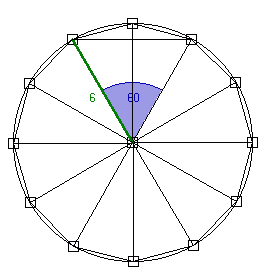
Wyznaczyć długość boku dwunastokąta foremnego wpisanego w okrąg o promieniu 6 cm.Rozwiązanie
 |
Możemy zauważyć, że gdy poprowadzimy linie (promienie) z każdego wierzchołka dwunastokąta foremnego do środka okręgu otrzymamy 12 identycznych trójkątów. Kąt (trójkąta) przy środku okręgu będzie wynosił 30o, a więc jeżeli połączymy dwa takie trójkąty, uzyskamy trójkąt o kącie 60o, a jak wiadomo jeżeli trójkąt ma miarę kąta 60o i dwa boki równe jest to trójkąt równoboczny. Aby wyglądało to przejrzyściej przerysujmy sam trójkąt (wraz z dwoma bokami dwunastokąta): |
| Oznaczmy bok dwunastokąta jako x. Jeżeli jest to trójkąt równoboczny (a jest, co wcześniej wyjaśniłam) to, jak sama nazwa wskazuje, wszystkie boki i kąty ma równe (co jest zaznaczone na rysunku obok). Wiadomo oczywiście, że a + b = 6 (bo również jest to promień koła) Teraz możemy wyliczyć z tw. Pitagorasa długość boku a: a2 + 32 = 62 a2 = 36 - 9 a = 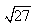 A teraz możemy policzyć b, ponieważ wiadomo, że a + b = 6, : b = 6 - 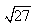 Teraz pozostaje już tylko wyliczenie x (z tw. Pitagorasa): x2 = 32 + b2 x2 = 9 + (6 - 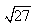 )2 )2x2 = 9 + (62 - 12 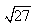 + 27) = 9 + 36 - 12 + 27) = 9 + 36 - 12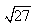 + 27 = 72 - 12 + 27 = 72 - 12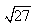 = 72 - 36 = 72 - 36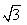 x = 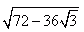 |
 |
| Teraz pozostaje już tylko wyliczenie x (z tw. Pitagorasa): x2 = 32 + b2 x2 = 9 + (6 - 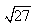 )2 )2x2 = 9 + (62 - 12 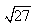 + 27) = 9 + 36 - 12 + 27) = 9 + 36 - 12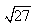 + 27 = 72 - 12 + 27 = 72 - 12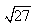 = = 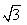 x = 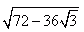 | |
Odpowiedź
Długość boku dwunastokąta foremnego wpisanego w okrąg o promieniu 6 cm wynosi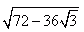 .
.
Autor:Agnieszka Biegun