LIGA ZADANIOWA UMK W TORUNIU 2004/2005
PREZENT WAKACYJNY DLA UCZNIÓW GIMNAZJUM

Zadanie 5

Wyznaczyć liczby całkowite a i b tak, by liczba a 4+ 4b4 była liczbą pierwszą.

Rozwiązanie:

a4 + 4b4=
= (a2)2 + (2b2)2 =
= (a2)2 + (2b2)2 + 2a2 * 2b2 - 2a2 * 2b2 =
= (a2 + 2b2)2 - 4a2b2 =
= (a2 + 2b2)2 - (2ab)2 =
= (a2 + 2b2 + 2ab)(a2 + 2b2 - 2ab)

Kiedy wynik iloczynu jest liczbą pierwszą jeden z czynników musi równać się 1.

Stąd:

a2+2b2- 2ab = 1/-b2
a2+ b2- 2ab = 1 - b2
(a-b)2=(1-b)(1+b)

a2+ 2b2+ 2ab = 1 /-b2
a2+ b2 +2ab = 1 - b
(a+b)2= (1-b)(1+b)

(a-b)2lub (a+b)2 jest zawsze liczbą nieujemną, więc iloczyn (1-b)(1+b) musi być liczbą nieujemną.

Tak więc:

1)Jeśli b="1"
(a-1)2= (1-1)(1+1)
(a-1)2= 0
a -1= 0
a = 1

(a+1)2= (1-1)(1+1)
(a+1)2= 0
a +1= 0
a = -1

2)Jeśli b= -1
[a-(-1)]2= [1-(-1)][1+(-1)]
(a+1)2= 0
a +1= 0
a = -1

[a+(-1)]2= [1-(-1)][1+(-1)]
(a-1)2= 0
a -1= 0
a = 1



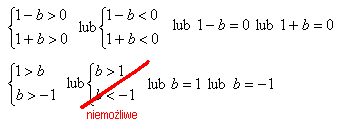
Odp.:(a="1" i b="1)" lub (a="-1" i b="-1)" lub (a="-1" i b="1)" lub (a="1" i b="-1).

Spr.:
Jeśli a="1" i b="1" to a4+ 4b4=5
Jeśli a="-1" i b="-1" to a4+ 4b4=5
Jeśli a="-1" i b="1" to a4+ 4b4=5
Jeśli a="1" i b="-1" to a4+ 4b4=5

Aleksander Bolesławski