LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM

Zadanie 5

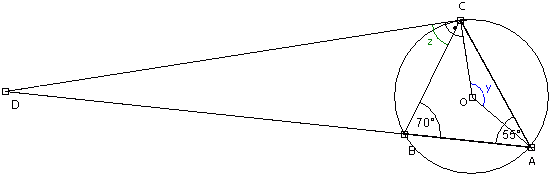
W okrąg wpisano trójkąt ABC, w którym kąt CAB = 55°, a kąt ABC = 70°. Przez punkt C poprowadzono styczną do okręgu. Styczna ta przecina przedłużenie boku AB w punkcie D. Oblicz miarę kąta ADC.

Rozwiązanie:

y = 2*70°=140° ponieważ kąt środkowy jest dwa razy większy od kąta wpisanego opartego na tym samym łuku.

|OCA| = (180°-140°) : 2 = 40° : 2 = 20°

|OCB| = |ACB| - |OCA|
|OCB| = 55°-20° = 35°

z = 90°- |OCB|
z = 90°-35° = 55°

|DBC| = 180°- |ABC|
|DBC| = 180° - 70°= 110°

|ADC| = 180° - |DBC| - z
|ADC| = 180° - 110° - 55° = 15°

Odpowiedź:

Miara kąta |ADC| równa się 15°.

Aleksander Bolesławski