LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM
Zadanie 11
W kwadracie ABCD poprowadzono dwa okręgi o środkach w wierzchołkach A i B i promieniu równym bokowi kwadratu. Okręgi te podzieliły kwadrat na cztery obszary. Oblicz pola i obwody tych obszarów, jeśli długość boku kwadratu jest równa 5 cm.
Rozwiązanie:
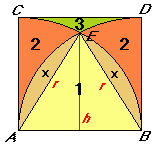 1) Kiedy połączymy wierzchołki A i B z punktem E, wówczas utworzy się trójkąt równoboczny ABE o bokach długości promienia koła. Wysokość tego trójkąta można wyliczyć z twierdzenia Pitagorasa:
1) Kiedy połączymy wierzchołki A i B z punktem E, wówczas utworzy się trójkąt równoboczny ABE o bokach długości promienia koła. Wysokość tego trójkąta można wyliczyć z twierdzenia Pitagorasa:
52 = h2 + 2,52
25 = h2 + 6,25
18,75 = h2
h = Ö18,75
h = 5Ö3 / 2
2) Teraz możemy obliczyć pole trójkąta AEB:
P = ah / 2
PAEB = 5 ´ 5Ö3 / 4
PAEB = 25Ö3 / 4
3) Obliczmy pole wycinka koła jaki tworzy jeden z kątów trójkąta AEB 60°:
Pa = a ´ pr2 / 360
P60° = 60 ´ 25p / 360
P60° = 25p / 6 cm2
4) Teraz można obliczyć pole figury x:
Px = P60° - PABE
Px = 25p / 6 - 25Ö3 / 4 cm2
5) Znając powierzchnię figury x możemy obliczyć pole pierwszej figury z zadania, które jest równe: PABE + 2Px. Oznaczmy ją F1.
F1 = PABE + 2Px
F1 = 25Ö3 / 4 + 2 ( 25p / 6 - 25Ö3 / 4 )
F1 = 25Ö3 / 4 + 25p/3 cm2
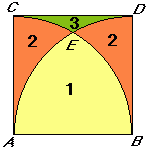 6) Możemy zauważyć, żę figura F1 i figura F2 razem tworzą ćwiartkę koła o promieniu 5cm. Jej pole będzie równe:
6) Możemy zauważyć, żę figura F1 i figura F2 razem tworzą ćwiartkę koła o promieniu 5cm. Jej pole będzie równe:
F1 + F2 = 1 / 4 pr2
F1 + F2 = 25 / 4 p cm2
7) Możemy obliczyć pole figury F2 odejmując od pola ćwiartki koła pole figury F1:
F2 = 25p / 4 - F1
F2 = 25p / 3 - ( 25p / 3 - 25Ö3 / 4 )
F2 = 25 / 4 ´ p - 25p / 3 + 25Ö3 / 4
F2 = 75 / 12 ´ p - 100p / 12 + 75Ö3 / 12
F2 = 75Ö3 / 12 - 25p / 12
F2 = 25 / 12 ( 3Ö3 - p ) cm2
8) Pole ostatniej figury F3 można obliczyć odejmując powierzchnię pozostałych trzech od pola kwadratu o boku 5 cm przedstawionego na rysunku powyżej:
Pkw = 5 ´ 5 = 25 cm2
F3 = Pkw - 2 ´ F2 - F1
F3 = 25 - 2 ´ 25 / 12 (3Ö3 - p ) - 25Ö3 / 4 + 25 p / 3 cm2
 9) Teraz policzmy obwód figury F1. Żeby to zrobić musimy wyliczyć długość łuku AE opartego na jednym z kątów trójkąta ABE.
9) Teraz policzmy obwód figury F1. Żeby to zrobić musimy wyliczyć długość łuku AE opartego na jednym z kątów trójkąta ABE.
60° ´ 2pr / 360° = 10p / 6 = 5p / 3
ObwF1 = 5p / 2 + 5p / 2 + 5 = 10p / 2 + 5 = 5p = 5 cm
10) Aby obliczyć obwód figury F2 należy policzyć długość łuku opartego na kącie 30°:
30° ´ p / 360° = 10p / 12 = 5p / 6
ObwF2 = 5p / 6 + 10p / 6 + 5 = 15p / 6 + 5 = 5p / 2 + 5 cm
11) Obwód figury F4 jest równy:
ObwF4 = 5p / 6 + 5p + 5 = 10p / 6 + 5 = 5p / 3 +5 cm
Małgorzata Hapyn ;)
 1) Kiedy połączymy wierzchołki A i B z punktem E, wówczas utworzy się trójkąt równoboczny ABE o bokach długości promienia koła. Wysokość tego trójkąta można wyliczyć z twierdzenia Pitagorasa:
1) Kiedy połączymy wierzchołki A i B z punktem E, wówczas utworzy się trójkąt równoboczny ABE o bokach długości promienia koła. Wysokość tego trójkąta można wyliczyć z twierdzenia Pitagorasa: 6) Możemy zauważyć, żę figura F1 i figura F2 razem tworzą ćwiartkę koła o promieniu 5cm. Jej pole będzie równe:
6) Możemy zauważyć, żę figura F1 i figura F2 razem tworzą ćwiartkę koła o promieniu 5cm. Jej pole będzie równe: 9) Teraz policzmy obwód figury F1. Żeby to zrobić musimy wyliczyć długość łuku AE opartego na jednym z kątów trójkąta ABE.
9) Teraz policzmy obwód figury F1. Żeby to zrobić musimy wyliczyć długość łuku AE opartego na jednym z kątów trójkąta ABE.