LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS II GIMNAZJUM
Zadanie 12
Oblicz.
a) 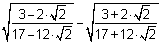
Rozwiązanie
Po przyjrzeniu się liczbom bez trudu zauważymy, iż można je przekształcić we wzory skróconego mnożenia na kwadrat sumy i kwadrat różnicy.
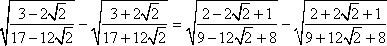
Przekształcamy dalej:
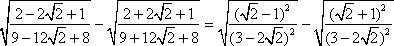
Kreska ułamkowa zastępuje znak mnożenia, a pierwiastek ilorazu równy jest ilorazowi pierwiastków, tak więc:
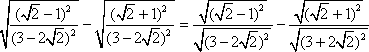
Kwadraty i pierwiastki "skracają się":
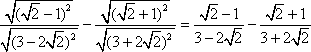
Teraz należy poszukać sposobu, aby usunąć niewymierność z mianowników ułamków. Najłatwiej pomnożyć każdy ułamek przez 1, przedstawione jako odpowiedni ułamek.
Korzystając z faktu, że w mianowniku pierwszego ułamka znajduje się różnica dwóch liczb, najlepiej pomnożyć go przez ułamek, w którego mianowniku znajdować się będzie suma tych dwóch liczb.
W mianowniku drugiegu ułamka mamy sumę dwóch liczb - pomnożymy więc przez ułamek, który w mianowniku będzie miał różnicę tych liczb.
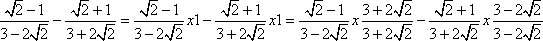
Łączymy mnożone ułamki w jeden:
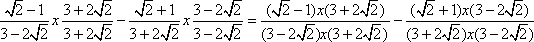
Wykonujemy działania w licznikach, a mianowniki przekształcamy zgodnie ze wzorem skróconego mnożenia: iloczyn sumy i różnicy dwóch liczb równy jest różnicy kwadratów tych liczb.
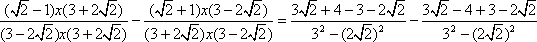
Upraszczamy licznik każdego z ułamków, po czym, jako że mają one takie same mianowniki, łączymy je w jeden i dokonujemy ostatnich obliczeń.
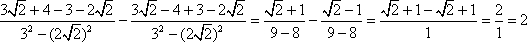
Odpowiedź
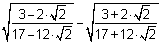 = 2.
= 2.
Artur Iwicki
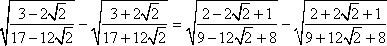
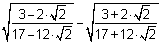
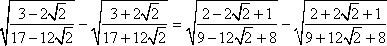
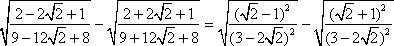
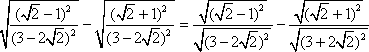
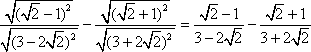
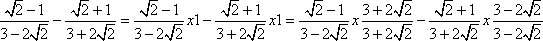
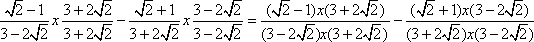
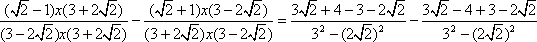
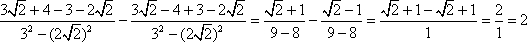
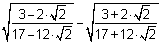 = 2.
= 2.