Brzeg trójkąta równobocznego o boku długości 10 cm "otoczono" zbiorem wszystkich punktow, które są odległe od co najmniej jednego z boków nie więcej niż o 1 cm. Oblicz pole tego zbioru oraz długość jego brzegu.
Rozwiązanie:
Zbiór punktów, który otacza trójkąt ABC od zewnątrz składa się z kilku części - 3 prostokątów i 3 wycinków koła - razem te wycinki tworzą jedno koło. Od strony wewnętrznej jest to trójkąt równoboczny, który składa się z 3 jednakowych trapezów.
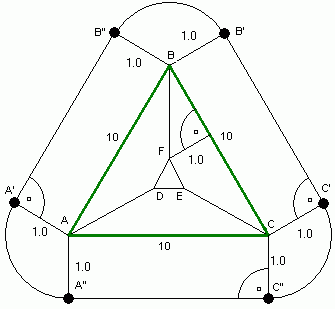
Pole zbioru otaczającego trójkąt ABC można obliczyć:
PBB''A'A + PBB'C'C + PACC''A'' + 3 × 1/3 × p × r2 = 30 + p (cm2)
Pole wewnętrznego zbioru punktów można obliczyć w ten sposób:
Zaznaczony wewnątrz trójkąt prostokątny jest polową trójkąta równobocznego o boku długości 2. Jego jego wysokość x można policzyć Z tw. Pitagorasa:
x2 + 12 = 22
x2 + 1 = 4
x2 = 3
x = Ö3
Mamy już długości podstaw
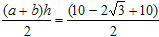
Pole całego kształtu równa się:
p + 30 + 3 ×
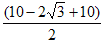 cm2
cm2Teraz wystarczy jeszcze obliczyć obwód tego zbioru (z wewnętrzną i zewnętrzną granicą)
3 × 10 + 2p × 1 + 3 × 8 = 30 + 2p + 24 = 54 + 2p (cm)
Odpowiedź:
Pole = p + 30 + 3 × 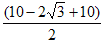 cm2
cm2
Obwód = 54 + 2p (cm)