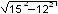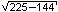Liga Zadaniowa UMK w Toruniu

LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM

Zadanie 14

Dany jest trójkąt równoramienny, w którym podstawa ma długość 24 cm, a ramię - długość 15 cm. Obliczyć odległość między środkami okręgu wpisanego w ten trójkąt i okręgu opisanego na tym trójkącie.

Rozwiązanie

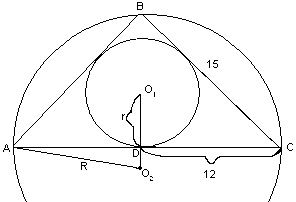|AD| = 12, |BO₂| = |AO₂| = R
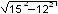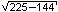|DO₂| = R - 9, |BD| =

= 9
12² + |DO₂|² = R²
12² + (R - 9)² = R²
144 + R² - 18R + 81 = R²
225 = 18R
R = 12,5
|DO₂| = 12,5 - 9 = 3,5

|O₁O₂| = |DO₂| + r

Pole trójkata ABC jest równe:

P = ½ ×|AC|×|BD| = ½ × 24×9 = 108

Z drugiej strony to samo pole jest równe sumie pól trójkątów AO₁C, CO₁B, BO₁A:

P = ½ ×|AC|× r + ½ ×|CB|× r + ½ ×|AB|× r

P = ½ × r (|AC| + |CB| + |AB|)

P = ½ × r (24 + 15 + 15)

P = 27 × r

Stąd

27 × r = 108

r = 4

|O₁O₂| = |DO₂| + r = 3,5 + 4 = 7,5

Odpowiedź

Odległość pomiędzy środkami okręgu wpisanego i okręgu opisanego wynosi 7,5 cm.

Tomasz Jankowski