LIGA ZADANIOWA UMK W TORUNIU 2004/2005
PREZENT WAKACYJNY DLA UCZNIÓW GIMNAZJUM

Zadanie 15

Znaleźć najmniejsze liczby naturalne a i b, przy czym b>1 takie, że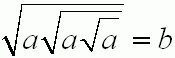

.

Rozwiązanie

Skorzystamy z ważnych praw dotyczących działań na pierwiastkach, których użyję w zadaniu: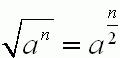

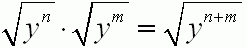
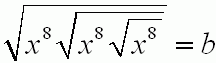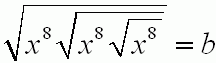
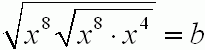
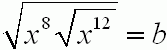
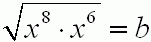
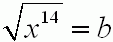
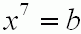
Podstawmy za a liczbę x 8, gdzie x Î N, czyli a="x" 8.
Otrzymujemy równanie:.

Wyliczamy je:

Liczba x jest najmniejszą liczbą naturalną różną od 1, czyli x="2," więc:
  1. a = 2 8 = 256
  2. b = 2 7 = 128

Grzegorz Jóźwiak

Klasa 2ag