LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM
Zadanie 15
Dany jest trójkąt OAB, gdzie A="(4," 0), B="(0," 4) i O="(0," 0). Niech
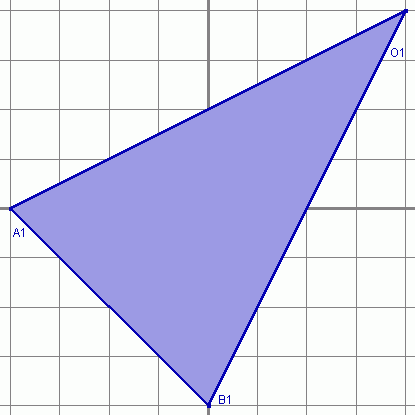
A1 będzie obrazem punktu A w symetrii osiowej względem
osi OB, B1 obrazem punktu B w symetrii osiowej względem
osi OA i O1 obrazem punktu O w symetrii osiowej względem
osi AB. Wyznaczyć pole trójkąta O1A1B1.
Narysuję trójkąt OAB:
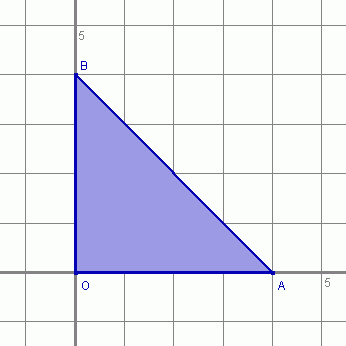
i trójkąt O1A1B1
:
Jest wiele sposobów na obliczenie pola trójkąta. Przedstawię jeden z nich. Pole trójkąta można
obliczyć jako pole kwadratu o wierzchołkach (-4, 4)(4, 4)(4, -4)(-4, -4) minus pole trójkąta o wierzchołkach
(-4, 0)(-4, -4)(0, -4) minus pole trójkąta o wierzchołkach (0, -4)(4, -4)(4, 4) minus pole trójkąta o wierzchołkach
(4, 4)(-4, 4)(-4, 0). Kwadrat ma bok 8, więc jego pole jest równe 8 × 8 = 64.
Pole trójkąta o wierzchołkach (-4, 0)(4, -4)(0, -4) jest równe 4 × 4 : 2 = 8.
Pole trójkąta o wierzchołkach (0, -4)(4, -4)(4, 4) jest równe 4 × 8 : 2 = 16.
Pole trójkąta o wierzchołkach (4, 4)(-4, 4)(-4, 0) jest równe 8 × 4 : 2 = 16.
Pole trójkąta O1A1B1 jest równe 64 - 8 - 16 - 16 = 24.
Grzegorz Jóźwiak
Klasa 2ag

