LIGA ZADANIOWA UMK W TORUNIU 2004/2005
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS I GIMNAZJUM
Zadanie 16
Dla jakich wartości m , z odcinków 2m + 2, m + 8, 3m + 1 , można zbudować trójkąt równoramienny?
Rozwiązanie:
Co to jest trójkąt równoranienny?
Jest to trójkąt, którego dwa (lub trzy) boki są tej samej długości. Boki o równej długości nazywamy ramionami, a trzeci bok - podstawą. Kąty wewnętrzne trójkąta równoramiennego między podstawą a ramionami mają równe miary.
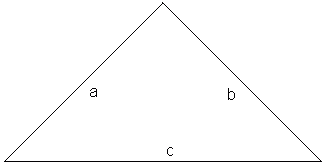
Na to aby z odcinków o danych długościach można było utworzyć trójkąt, muszą być spełniona nierówność trójkąta, tzn. suma długości dwóch krótszych odcinków musi być większa niż długość trzeciego odcinka.Oznaczę długości ramion trójkąta równoramiennego literami a i b (a = b) , a podstawę literą c:

Przypadek 1:
a="2m+2
b="m+8
c="3m+1
2m+2="m+8/-m
m+2="8/-2
m="6
Sprawdzenie:
a="14,b=14,c=19
28>19 Może tak być.
Przypadek 2:
a="m+8
b="3m+1
c="2m+2
m+8="3m+1/-m
8="2m+1/-1
7="2m/:2
3,5="m
m="3,5
Sprawdzenie:
a="11,5" ,b="11,5" ,c="9
23>9 Może tak być.
Przypadek 3:
a="3m+1
b="2m+2
c="m+8
3m+1="2m+2/-2m
m+1="2/-1
m="1
Sprawdzenie:
a="4,b=4,c=9
8<9 Nie może tak być.
Odpowiedź:Trójkąt równoramienny można zbudować w przypadku kiedy m równa się 6 lub 3,5.
Joanna Karnowska