LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA NIESPODZIANKI
DLA KLAS II GIMNAZJUM

Zadanie 1c

Rozwiąż równanie na liczbach całkowitych:

xy = 2003(x + y)

Rozwiązanie:

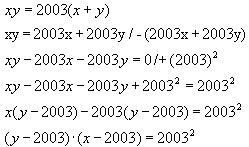
2003 jest liczbą pierwszą więc mamy ograniczoną liczbę możliwości przedstawienia liczby 20032 w postaci iloczynu dwóch liczb całkowitych:

  1. 1 × 20032 = 20032

    y - 2003 = 1 i x - 2003 = 20032
    y = 2004 i x = 20032 + 2003

  2. 2003 × 2003 = 20032

    y - 2003 = 2003 i x - 2003 = 2003
    y = 4006 i x = 4006

  3. 20032 × 1 = 20032

    y - 2003 = 20032 i x - 2003 = 1
    y = 20032 + 2003 i x = 2004

  4. (-1) × (-20032) = 20032

    y - 2003 = -1 i x - 2003 = -20032
    y = 2002 i x = -20032 + 2003

  5. (-2003) × (-2003) = 20032

    y - 2003 = -2003 i x - 2003 = -2003
    y = 0 i x = 0

  6. (-20032) × (-1) = 20032

    y - 2003 = -20032 i x - 2003 = -1
    y = -20032 + 2003 i x = 2002

Joanna Karnowska