LIGA ZADANIOWA UMK W TORUNIU 2004/2005
PREZENT WAKACYJNY DLA UCZNIÓW GIMNAZJUM

Zadanie 18:

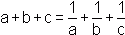Uzasadnić, że jeśli abc = 1 i , to co najmniej jedna spośród liczb a, b, c jest równa 1.

Rozwiązanie:

1. Z treści zadania wynika, że: a ą 0, b ą 0, c ą 0, (bo gdyby jedna z liczb w iloczynie abc była równa zero to iloczyn nie mógłby być równy 1.)

2.

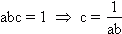
3.

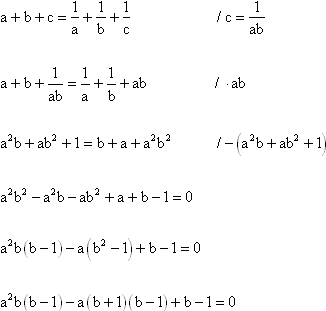
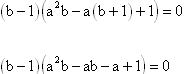
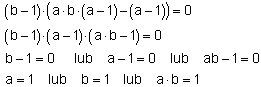
Poniważ c jest odwrotnością ab, więc ostatecznie otrzymujemy, że

a = 1 lub b = 1 lub c = 1.

Agata Kwapisz