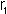 będzie promieniem okręgu wpisanego w trójkąt ADC,
będzie promieniem okręgu wpisanego w trójkąt ADC, 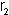 - promieniem okręgu wpisanego w trójkąt BDC, r - promieniem okręgu wpisanego w trójkąt ABC, zaś
- promieniem okręgu wpisanego w trójkąt BDC, r - promieniem okręgu wpisanego w trójkąt ABC, zaś 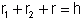 .
.LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM
Zadanie 18:
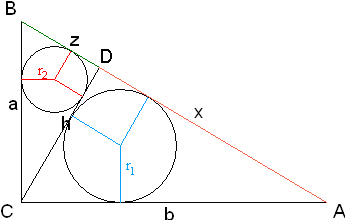
W trójkącie prostokątnym ABC o kącie prostym przy wierzchołku C poprowadzono wysokość CD. Niech 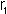 będzie promieniem okręgu wpisanego w trójkąt ADC,
będzie promieniem okręgu wpisanego w trójkąt ADC, 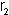 - promieniem okręgu wpisanego w trójkąt BDC, r - promieniem okręgu wpisanego w trójkąt ABC, zaś
- promieniem okręgu wpisanego w trójkąt BDC, r - promieniem okręgu wpisanego w trójkąt ABC, zaś 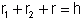 .
.
ROZWIĄZANIE:
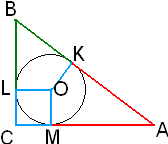
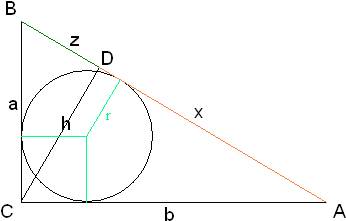
Niech R oznacza promień okręgu wpisanego w trójkąt prostokątny ABC
Punkty K, L, M są punktami styczności okręgu z bokami trójkąta. Stąd:
|AK| = |AM| oraz |BK| = |BL|.
Czworokąt OLCM to kwadrat, więc
|CM| = |CL| = R.
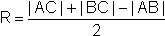
Przechodę teraz do zadania.
Zastosuję podaną wyżej własność do wszystkich trzech trójkątów o których mowa w zadaniu.
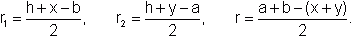
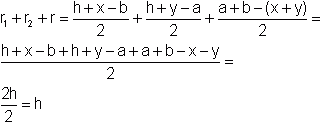
AGATA KWAPISZ