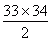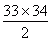LIGA ZADANIOWA UMK W TORUNIU 2004/2005
PREZENT WAKACYJNY DLA UCZNIÓW GIMNAZJUM
Zadanie 19
Czy zbiór liczb naturalnych 1, 2, 3, ..., 33 można podzielić na 11 grup po trzy liczby tak, by w każdej grupie jedna z liczb była równa sumie dwóch pozostałych?
Rozwiązanie
Przypuścmy, że jest to możliwe i liczby od 1 do 33 zostały rozbite na następuące grupy:
Grupa 1: {a1,b1,c1} gdzie c1=a1+b1
Grupa 2: {a2,b2,c2} gdzie c2=a2+b2
...
...
...
Grupa 11: {a11,b11,c11} gdzie c11=a11+b11
(1) Możemy teraz te wszystkie liczby dodać:
1 + 2 + 3 + ... + 33 =
= (a1 + a2 + ... + a11) +
(b1 + b2 + ...+ b11)+
(c1 + c2 + ... + c11) =
= (a1 + b1 ) + (a2 + b2 ) + ... + (a11 + b11 ) + (c1 + c2 + ... + c11) =
= (c1 + c2 + ... + c11) + (c1 + c2 + ... + c11)
= 2×(c1 + c2 + ... + c11)
Wynik ten jest liczba parzystą (gdyż całkowitą wielokrotnoscią liczby 2).
(2)
Z drugiej strony sumę liczb 1 + 2 + 3 + ... + 33 możemy wyliczyć konkretnie:
Niech:
| | S | = | 1 | + | 2 | + | 3 | + | ... | + | 30 | + | 31 | + | 32 | + | 33 |
| + | S | = | 33 | + | 32 | + | 31 | + | ... | + | 30 | + | 3 | + | 2 | + | 1 |
|
| + | 2S | = | 34 | + | 34 | + | 34 | + | ... | + | 34 | + | 34 | + | 34 | + | 34 |
Stąd:
2S = 33 × 34
S = 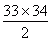
S = 33 × 17
Wynikiem S tego mnożenia będzie liczba nieparzysta, ponieważ jeżeli czynniki są nieparzyste to wynik mnożenia też jest nieparzysty.
Podsumowanie
(1) 1 + 2 + ... + 33 = 2×(c1 + c2 + ... + c11) liczba parzysta
(2) 1 + 2 + ... + 33 = 33 × 17 liczba nieparzysta
Otrzymaliśmy, że ta sama suma jest jednocześnie parzysta i nieparzysta.
To jest niemożliwe.
Kuba Ładysz