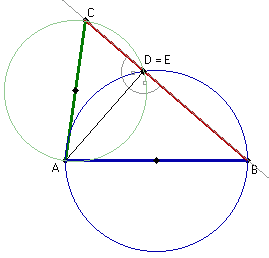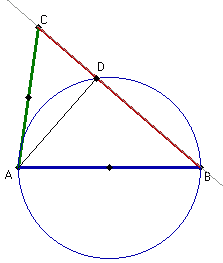
Zatem kąt ADB musi być prosty.
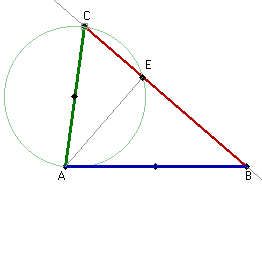
Zatem kąt AEC musi być prosty.
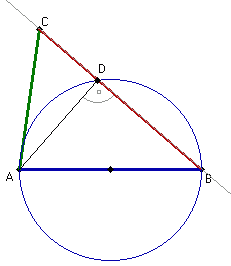
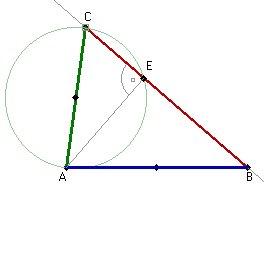
Wniosek:
Punkt D leży na prostej BC i odcinek AD jest prostopadły do prostej BC.Wniosek:
Punkt E leży na prostej BC i odcinek AE jest prostopadły do prostej BC.Ale jak wiadomo, z punktu A można poprowadzić tylko jeden odcinek prostopadły do prostej BC. Wynika stąd, że punkty D i E muszą być tymi samymi punktami, tzn.