LIGA ZADANIOWA UMK W TORUNIU 2004/2005
ZADANIA KONKURSOWE Z ETAPU I
DLA KLAS I GIMNAZJUM

Zadanie 4

Czy wśród liczb naturalnych od 1 do 2004 włącznie więcej jest liczb podzielnych przez 5, czy też liczb, które będą dzielić się przez 9 lub przez 11?

Rozwiązanie:

Ilość liczb naturalnych od 1 do 2004 podzielnych przez 5 można obliczyć w następujący sposób:

2004 = 400×5 + 4

Zbiór liczb podzielnych przez 5 wyglądać będzie następująco (przyjmijmy literkę P jako oznaczenie tego zbioru):

P={1×5, 2×5, 3×5,...,400×5}

Liczb naturalnych podzielnych przez 5 jest 400.

Musimy obliczyć ilość liczb naturalnych od 1 do 2004 podzielnych przez 9 i 11.

W przypadku cyfry 9, liczbę 2004 możemy przedstawić jako:

2004 = 222×9 + 6,

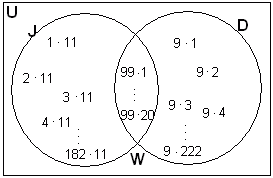
Czyli zbiór liczb podzielnych przez 9 wygląda następująco (zbiór oznaczam literką D):

D = {1×9, 2×9, 3×9,..., 222×9}

Liczb naturalnych podzielnych przez 9 jest 222.

Ilość liczb podzielnych przez 11 obliczymy w taki sam sposób, czyli:
Liczbę 2004 można przedstawić jako

2004 = 182×11 + 2,

czyli zbiór liczb podzielnych przez 11 wygląda następująco (zbiór oznaczam literką J):

J={1×11, 2×11, 3×11,..., 182×11}

Liczb naturalnych podzielnych przez 11 jest 182.

Teraz należy obliczyć ile jest liczb naturalnych podzielnych przez 11 i 9.

Jeśli liczba jest podzielna przez 9 i 11 to musi być podzielna przez 99.

Liczbę 2004 możemy przedstawić jako:

2004 = 20×99 + 24

Zbiór liczb podzielnych przez 9 i 11 wygląda następująco (oznaczam go literką W):

W={1×99, 2×99, 3×99,..., 20×99}

Liczb podzielnych przez 11 i 9 jest 20.

Ilość liczb podzielnych przez 11 i 9 można teraz przedstawić graficznie za pomocą zbiorów (przyjmijmy oznaczenia takie jakie wykorzystałam przy rozwiązywaniu zadania):

J ma 182 elementy; D ma 222 elementy, W ma 20 elementów.

Możemy teraz policzyć ile jest liczb podzielnych przez 9 lub 11

182 + 222 - 20 = 404 - 20 = 384

Łączna ilość liczb podzielnych przez 9 i 11 to 384.

Odpowiedź:

324 < 400
Liczb podzielnych przez 9 lub 11 jest mniej niż liczb podzielnych przez 5.

Marlena Rozenberg kl. Ia