LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA KONKURSOWE Z ETAPU III
DLA KLAS II GIMNAZJUM

Zadanie 4

Dany jest trójkąt OAB, gdzie A = (-8,0), B = (0,-8) i O = (0,0). Niech A₁ będzie obrazem punktu A w symetrii osiowej względem prostej OB, B₁ obrazem punktu B w symetrii osiowej względem prostej OA i O₁ będzie obrazem punktu O w symetrii osiowej względem prostej AB. Wyznacz pole trójkąta O₁A₁B₁.

Rozwiązanie

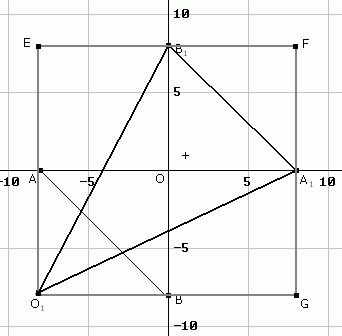
Najprostszym rozwiązaniem tego zadania jest opisanie na trójkącie prostokątu, po czym kolejno odejmować od pola prostokąta pola wiadomych trójkątów. (rysunek niżej)
P_O₁A₁B₁=P_O₁GFE-(P_O₁EB₁+P_B₁FA₁+P_O₁A₁G)
P_O₁GFE=16×16=256 (J²)
P_O₁EB₁=a×h_/2=16×8_/2=64(J²)
P_O₁A₁G=16×8_/2=64(J²)
P_O₁EB₁=P_O₁A₁G
P_B₁FA₁=8×8_/2=32 (J²)
P_O₁A₁B₁=256-(64+64+32)=256-160=96 (J²)
Rozmiar: 5726 bajtów

Odpowiedź:

Pole trójkąta P_O₁A₁B₁ wynosi 96 (J²).

Marlena Rozenberg kl. IIa