Zadanie 6

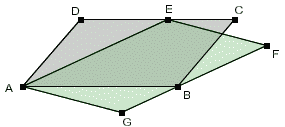
Uzasadnij, że równoległoboki ABCD i AEFG mają równe pola.

ROZWIĄZANIE

Jeśli połączę odcinkiem punkty E i B, to otrzymam trójkąt ABE.

• Przyjmując AB za podstawę trójkąta ABE, jego wysokość będzie jednocześnie wysokością równoległoboku ABCD o podstawie AB. Stąd pole równolegloboku ABCD jest dwa razy większe od pola trójkata ABE.
  
  
• Przyjmując AE za podstawę trójkąta ABE, jego wysokość będzie jednocześnie wysokością równoległoboku AEFG o podstawie AE. Stąd pole równolegloboku AEFG jest dwa razy większe od pola trójkata ABE.

Tytus Szabelski