2a(a + 2b) = b(a + 2b)
2a(a + 2b) - b(a + 2b) = 0
(a + 2b)(2a - b) = 0
a + 2b = 0 lub 2a - b = 0
a = -2b lub 2a = b
a = -2b lub b = 2a
- Jeśli a = -2b, to:
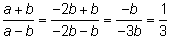
- Jeśli b = 2a, to:
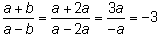
Odpowiedź:
LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS VI SZKÓŁ PODSTAWOWYCH
Zadanie 14
Obliczyć wartość ułamka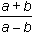 jeśli 2a2 + 4ab = ab + 2b2.
jeśli 2a2 + 4ab = ab + 2b2.
Rozwiązanie
To zadanie można rozwiązać bardzo prosto. Wystarczy tylko z 2a2+4ab="ab+2b
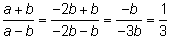
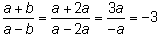
Odpowiedź:
Wartość danego ułamka wynosi albo 1/3 albo -3.Autor: Katarzyna Truszkowska