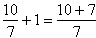
Zgadza się bo:
NWD(10,7)=1 i NWD (10+7,7)=1
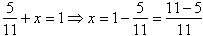
Zgadza się bo:
NWD(5,11)=1 i NWD (11-5,11)=1
LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA NIESPODZIANKI
DLA KLAS VI SZKÓŁ PODSTAWOWYCH
Rozwiązanie
Sprawdziłam najpierw na przykładach jak to działa:
| 12a | 12b |
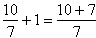 Zgadza się bo: NWD(10,7)=1 i NWD (10+7,7)=1 |
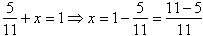
Zgadza się bo: NWD(5,11)=1 i NWD (11-5,11)=1 |
ad a)
Gdyby ułamek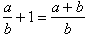 był skracalny, to:
był skracalny, to:
NWD(a, a + b) = d ą 1
a = da' gdzie a' jest jakąś liczbą całkowitą..
a + b = db' gdzie b' jest jakąś liczbą całkowitą. .
b = (a + b) - a = db' - da' = d(b' - a')
i ułamek 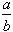 jest skracalny przez liczbę d.
jest skracalny przez liczbę d.
ad b)
Gdyby ułamek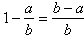 był skracalny, to:
był skracalny, to:
NWD(a, a + b) = D ą 1
b = Db'' gdzie b'' jest jakąś liczbą całkowitą.
b - a = Da'' gdzie a'' jest jakąś liczbą całkowitą. .
a = b - (b - a) = Db'' - Da'' = D(b'' - a'')
i ułamek 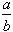 jest skracalny przez liczbę D.
jest skracalny przez liczbę D.
Autor: Katarzyna Truszkowska