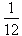 okręgu tarczy zegara;
okręgu tarczy zegara;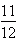 okręgu tarczy zegara.
okręgu tarczy zegara.LIGA ZADANIOWA UMK W TORUNIU 2004/2005
PREZENT WAKACYJNY DLA ABSOLWENTÓW SZKÓŁ PODSTAWOWYCH
Zadanie 3
Ile razy w ciągu doby wskazówki minutowa i godzinowa tworzą kąt prosty?
W ciągu jednej godziny:
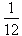 okręgu tarczy zegara;
okręgu tarczy zegara;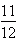 okręgu tarczy zegara.
okręgu tarczy zegara.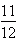 okręgu tarczy zegara.
okręgu tarczy zegara.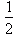 okręgu.
okręgu.
|
W początkowym położeniu:
Wobec tego w czasie t:
|
Możemy teraz policzyć najkrótszy odcinek czasu t jaki musi upłynąć aby wskazówka minutowa i godzinowa ustawiły się ponownie pod kątem prostym jeśli na początku także były ustawione pod kątem protym:
t × 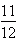 okręgu =
okręgu = 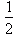 okręgu.
okręgu.
t × 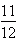 =
= 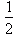
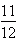 :
:
t = 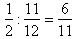 (godziny)
(godziny)
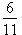 godziny wskazówki ustawiają się pod katem prostym.
godziny wskazówki ustawiają się pod katem prostym. Odpowiedź na zadanie uzyskamy dzieląc ilość godzin upływających w ciągu doby przez czas, po którym wskazówki tworzą kolejny kąt prosty.
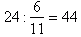
Odpowiedź: W ciągu doby wskazówki minutowa i godzinowa utworza kat prosty 44 razy.
Agata Wiklendt