LIGA ZADANIOWA UMK W TORUNIU 2004/2005
ZADANIA KONKURSOWE Z ETAPU I
DLA KLAS VI SZKÓŁ PODSTAWOWYCH
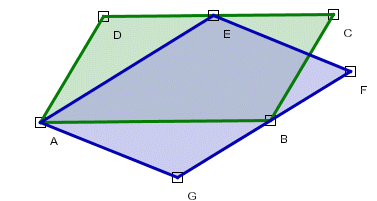
Wprowadźmy dodatkowe oznaczenia, takie jak na rysunku:
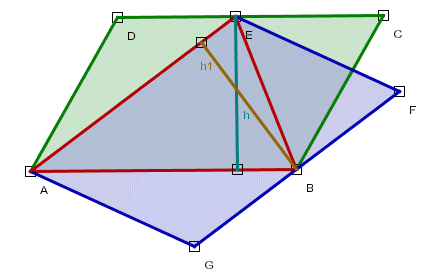
Możemy zauważyć, że trójkąt ABE jest wspólny dla obydwóch trójkątów. Jego pole możemy policzyć:
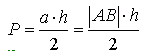
Natomiast pole równoległoboku ABCD:
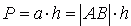
Wyraźnie widzimy, że pole trójkąta ABE jest połową pola równoległoboku ABCD.
Pole trójkąta ABE można także policzyć w inny sposób:
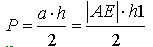
Natomiast pole równoległoboku AGFE:
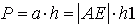
Mamy podobną sytuację. Pole trójkąta ABE jest połową pola równoległoboku AGFE.
Skoro pole trójkąta ABE jest połową pola każdego z równoległoboków to znaczy,że pola tych równoległoboków są równe!
Karolina Żółtewicz