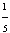 okręgu.
okręgu.
LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM
Oblicz miary kątów trójkąta równoramiennego, którego wierzchołki leżą na okręgu wiedząc, że jeden z boków jest oparty na 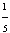 okręgu.
okręgu.
Rozwiązanie
Jeśli jeden z boków trójkąta leży na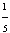 długości okręgu, możemy posłużyć się pięciokątem foremnym.
długości okręgu, możemy posłużyć się pięciokątem foremnym.
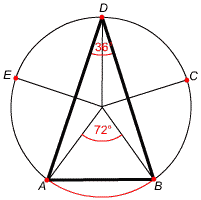 | 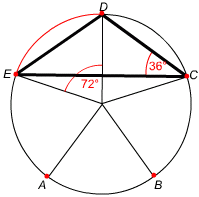 |
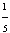 długości okręgu, daje 72°.
Zastosujmy twierdzenie, które mówi, że kąt wpisany równa się dwóm kątom środkowym:
długości okręgu, daje 72°.
Zastosujmy twierdzenie, które mówi, że kąt wpisany równa się dwóm kątom środkowym: 72° : 2 = 36°
więc kąt y ma miarę równą 36° lub kąt z ma miarę równą 36° .| I | II | ||
Jeśli y ma miarę równą 36° to ponieważ kąty przy podstawie trójkąta mają tę samą rozwartość, otrzymamy: z = (180° - 36°) : 2 = 144 : 2 = 72° |
Jeśli z ma miarę równą 36° to ponieważ kąty przy podstawie trójkąta mają tę samą rozwartość, otrzymamy: y = 180° - 2z = 180° - 2×36° = 108° |
Odpowiedź: Ostatecznie trójkat ten może miać kąty o miarach:
y = 36°, z = 72° i z = 72° lub y = 108°, z = 36° i z = 36°.
Izabella Grzebieniak
KLASA IA
