Rysujemy i oznaczamy odcinek SA o współrzędnych S="(0,0)i" A="(2,-2).
Rysujemy odcinek CS symetryczny do odcinka SA o współrzędnych C="(-2,2)i" S="(0,0).
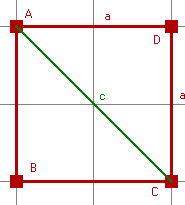
Dla ułatwienia rysujemy teraz kwadrat o wierzchołkach w punktach A,C oraz A' i C', gdzie A'=(-2,-2) a C'=(2,2).
Cały odcinek AC oznaczamy teraz jako f1, gdyż jest on przekątną powstałego kwadratu oraz jedną z przekątnych naszego rombu.
Bok kwadratu AA'CC' jest równy 4, a przekątną kwadratu możemy obliczyć z podanego wcześniej wzoru: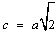 ,gdzie "c" jest u nas przekątną f1(jak również odcinkiem AC),natomiast "a" jest bokiem kwadratu. Z tego otrzymujemy, że ,gdzie "c" jest u nas przekątną f1(jak również odcinkiem AC),natomiast "a" jest bokiem kwadratu. Z tego otrzymujemy, że 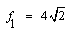
Wiemy, że Pole rombu = ½ × f1 × f2 , gdzie 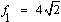 , a f2 jest drugą przekątną naszego rombu. Przekształcamy wzór i obliczamy długość f2. Zatem , a f2 jest drugą przekątną naszego rombu. Przekształcamy wzór i obliczamy długość f2. Zatem
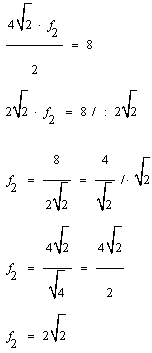
Możemy teraz stwierdzić że skoro 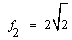 to przekątna o tej długości jest ona również przekątną kwadratu o boku 2 bo (korzystamy z tego samego wzoru) to przekątna o tej długości jest ona również przekątną kwadratu o boku 2 bo (korzystamy z tego samego wzoru)
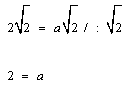
Na osi współrzędnych rysujemy kwadrat o boku długości 2, ze środkiem w punkcie S="(0,0)," oznaczając wierzchołki jako B,B',D,D', gdzie B="(1,1)," B'=(-1,1), D="(-1,-1)," D'=(1,-1).
Rysujemy przekątną BD tego kwadratu, która jest równocześnie krótszą przekątną rombu, czyli f2.
Łączymy teraz wszystkie wierzchołki rombu ABCD, (które są zakończeniami przekątnych f1 i f2). | 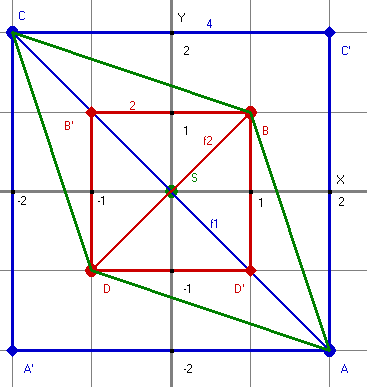
|
 Do wykonania zadania potrzebna będzie nam informacja że przekątna kwadratu wyraża się wzorem
Do wykonania zadania potrzebna będzie nam informacja że przekątna kwadratu wyraża się wzorem 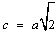
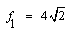
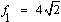 , a f2 jest drugą przekątną naszego rombu. Przekształcamy wzór i obliczamy długość f2. Zatem
, a f2 jest drugą przekątną naszego rombu. Przekształcamy wzór i obliczamy długość f2. Zatem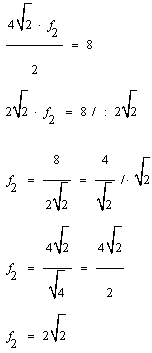
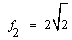 to przekątna o tej długości jest ona również przekątną kwadratu o boku 2 bo (korzystamy z tego samego wzoru)
to przekątna o tej długości jest ona również przekątną kwadratu o boku 2 bo (korzystamy z tego samego wzoru)