LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA NIESPODZIANKI
DLA KLAS I GIMNAZJUM

Zadanie 6

Figura przedstawiona na rysunku złożona jest z sześciu kwadratów jednostkowych. Jej obwód jest równy 12.

Czy można do niej dołączyć jeszcze kilka kwadratów jednostkowych, aby obwód otrzymanej figury był równy 18?

Nowy kwadrat jednostkowy można dołączyć tylko tak, aby przynajmniej jeden jego bok nakładał się na bok poprzedniego kwadratu i aby w figurze nie powstawały "dziury".
  1. Ile najmniej kwadratów jednostkowych potrzeba, aby to osiągnąć?
  2. Ile najwięcej kwadratów jednostkowych potrzeba, aby to osiągnąć?

Rozmiar: 190 bajtów

Rozwiązanie

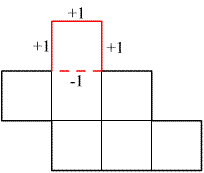  1. Jeśli figura złożona z kwadracików jednostkowych nie ma "dziur", to po dodaniu jednego kwadratu jednostkowego zyskujemy maksymalnie 2 odcinki jednostkowe obwodu, bo przynajmniej jeden odcinek poprzedniej figury znika (ten wzdłuż, którego doklejamy) a pojawiają się dodatko nawyżej trzy nowe odcinki (4 minus 1 wzdłuż, którego doklejamy).

    Jeżeli obwód wynosi 12 to do 18 brakuje nam 6 odcinków jednostkowych obwodu, a więc musimy dokleić conajmniej 3 kwadraciki bo 6:2=3.

    Oto przykład jak to zrobić:


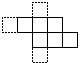
  2. Przez dostawienie jednego kwadracika możemy też nie zmienić liczby krawędzi odcinków jednostkowych obwoedu.
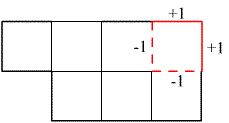    Taka sytuacja może nastąpić na początku tylko 2 razy.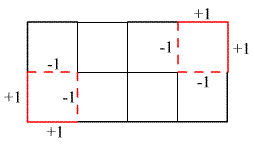
    Dodanie teraz poziomego "pasa" 4 kwadracików, zwiekszy liczbę krawędzi zaledwi o 2. Możemy więc to zrobić trzy razy. W ten sposób mamy rozwiazanie z największą liczbą (14) doklejonych kwadracików:

Opowiedzi: Tak. (a) 6. (b) 14.

Karolina Gwizdała