LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM

Zadanie 8

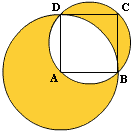Na kwadracie ABCD o boku 5 opisano okrąg, a następnie wykreślono okrąg o środku w punkcie A i promieniu AB. Oblicz pole kolorowej figury widocznej na rysunku.

Rozwiązanie

Oznaczamy:
pole kwadratu jako Pk
pole dużego koła jako Pd
pole małeko koła jako Pm
pole zakolorowanego obszaru jako Pz.

|AB|=|BC|=|CD|=|DA|=5cm

1.Liczymy pole dużego koła:

Pd= pr2= p52=25p

2.Za pomocą tw. Pitagorasa (a^2+b^2=c^2) liczymy pole małego koła. Najpierw obliczamy promień koła: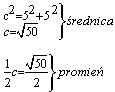

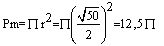
A następnie jego pole:

3.Liczymy pole kwadratu, a nastepnie różnicę pola małego koła i pola kwadratu. Następnie dzielimy uzyskany wynik na dwa uzyskując pola y i z (są one taki same):

Pk=25

4.Obliczamy x:

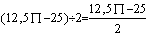
x=Pk-1/4*Pd
x=25-1/4*25p
x=25-6,25p

5.Obliczamy pole zakolorowanego obszaru:

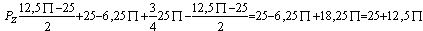
Odpowiedź

Pole zakolorowanego obszaru wynosi 25+12,5p.

Karolina Gwizdała