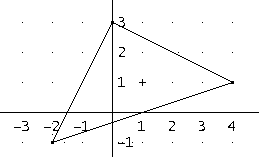
LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM
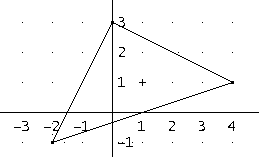
Pierwszy równoległobok:
Należy odbić symetrycznie wierzchołek (-2,-1) względem środka przeciwległego boku: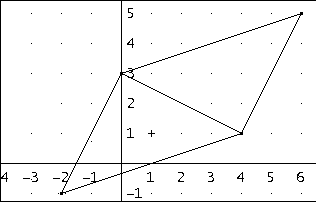
Drugi równoległobok:
Należy odbić symetrycznie wierzchołek (4,1) względem środka przeciwległego boku.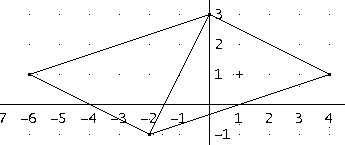
Trzeci równoległobok:
Należy odbić symetrycznie wierzchołek (0,3) względem środka przeciwległego boku.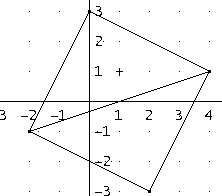
Zakończyliśmy więc pierwszą część zadania. Teraz trzeba obliczyć pola naszych równoległoboków.
Zacznijmy od tego, że każdy z tych równoległoboków ma te samo pole, więc jeżeli obliczymy pole jednego z nich, to będziemy mieli pole pozostałych.
Obliczmy więc pole np. pierwszego równoległoboku.
Aby obliczyć jego pole możemy:
-zamknąć nasz równoległobok w prostokącie (tak jak na rysunku):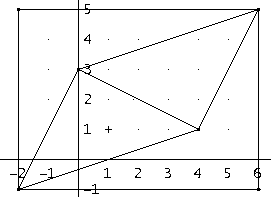
6j x 8j= 48j2
-obliczyć pola figur, które znajdują się w prostokącie, ale nie są w równoległoboku: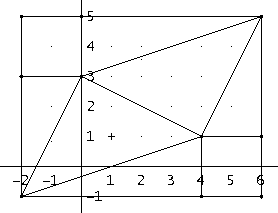
2j * 2j = 4j2
2j * 2j = 4j2
4j * 2j * 0,5 = 4j2
4j * 2j * 0,5 = 4j2
6j * 2j * 0,5 = 6j2
6j * 2j * 0,5 = 6j2
(4j2 * 4) + (2 * 6j2) = 24j2
-odjąć od pola "dużego" prostokąta pola figur, które znajdują się w prostokącie, ale nie są w równoległoboku48j2 - 24j2 = 24j2
ODPOWIEDŹ:
Istnieją 3 równoległoboki o podanych właściwościach.FILIP IDZIKOWSKI