LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM
Zadanie 9
Wysokość opuszczona z wierzchołka kąta prostego dzieli przeciwprostokątną na
odcinki długości 4 cm i 16 cm. Oblicz pole i obwód tego trójkąta.
Rozwiązanie:
Przyjmijmy oznaczenia jak na rysunku
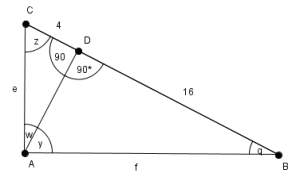
Suma kątów w trójkącie musi wynosić 90 stopni, więc:
q + y = 90 stopni
z + w = 90 stopni
z + q = 90 stopni
więc:
w = q
90 + z + w = 90 + q + y /-90 - q
z = y
Z cechy kkk (kąt, kąt, kąt) wynika, że trójkąty ACD i ABD są podobne.
4/x = x/16 /*x *16
64 = x2 / pierwiastkujemy obie strony równania
8 = x
Teraz możemy policzyć pole trójkąta ABC:
Pole trójkąta ACD: 4 cm * 8 cm * 0,5 = 16 cm2
Pole trójkąta ABD: 8 cm * 16 cm * 0,5 = 64 cm2
64 cm2 + 16 cm2 = 80 cm2
Pole trójkąta ABC wynosi 80 cm2
Teraz policzmy obwód trójkąta ABC:
Z tw. Pitagorasa:
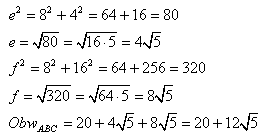
Odpowiedź:
Pole trójkąta ABC wynosi 80 cm2, a jego obwód wynosi 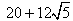 .
.
FILIP IDZIKOWSKI

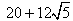 .
.