LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM

Zadanie 10

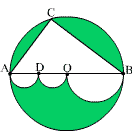Średnica AB dzieli koło o środku w punkcie O na dwie części. Trójkąt prostokątny ABC ma przyprostokątne długości 18 cm i 24 cm.Punkt D będzie środkiem odcinka AO. Na odcinkach AD, DO i OB zbudowano jako na średnicach półkola tak, jak to widać na rysunku.Oblicz pole i obwód kolorowego obszaru.

Rozwiązanie

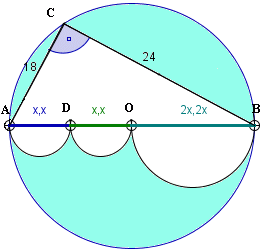
|AB|= 8x
242+182=(8x)2
576+324=(8x)2
900=(8x)2/pierwiastkujemy strony równania
30=8x     /:8
x=30/8
x=15/4
|AO|=r=4x=15

Pole:
 Pzakolorowane=p(4x) 2-px2-1/2p(2x)2-(|AC|*|CB|):2
P=p*[4*(15/4)]2 -p(15/4)2-1/2 p[2*(15/4)]2-24*18*1/2
P=p225-p 225/16-1/2p56,25-216
P=225p -14 1/16 p- 28 1/8 p - 216 = 182 13/16p-216 p

Obwód:
Obw = 2p*15 = 30p = 1 (2p*7,5) = 1 (15p) = 7,5 p = 2p*3,75 = 7,5 p
Obw.zakolorowanego obszaru= 30p + 7,5p + 7,5p + 18 + 24 = 45p + 42

Odpowiedź

Pole kolorowego obszaru wynosi 182 13/16p-216 ,
a obwód wynosi 45p + 42.

Wykonała Olivia Klepacka kl. IIa