x - część okręgu taka, że:
łukAB = 3x,
łukBC = 6x,
łukCD = 5x,
łukDA = 4x.
Na początku obliczamy długości łuków x mieści okrąg 3x + 6x + 5x + 4x = 18x
Obliczamy teraz ile stopni ma kąt środkowy oparty na łuku x:
360:18="
Obliczamy teraz ile stopni mają kąty środkowe oparte na łukach:
AB: 3x="3×20°" = 60°
BC: 6x="6×20°" = 120°
CD: 5x="5×20°" = 100°
DA: 4x="4×20°" = 80°
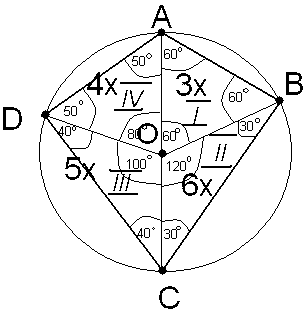
Widzimy na rysunku, że trójkąt I jest równoboczny co oznacza, że jego wszystkie kąty mają miarę 60°.
Widzimy również na rysunku, że trójkąty II, III, IV są równoramienne, więc:
kąty CBO i BOC mają po 30°, bo 180° - 120° = 60° i 60°:2 = 30°
kąty DCO i CDO mają po 40°, bo 180° - 100° = 80° i 80°:2 = 40°.
kąty ADO i DAO mają po 50°, bo 180° - 80° = 100° i 100°:2 = 50°
Teraz tylko wystarczy dodać miary kątów o wspólnych wierchołkach, aby otrzymać miary kątów czworokąta ABCD.
A więc:
kąt ABC ma 60° + 30° = 90°
kąt BCD ma 30° + 40° = 70°
kąt CDA ma 40° + 50° = 90°
kąt BCD ma 50° + 60° = 110°