LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM
Zadanie 13
Wyznaczyć pole i obwód ośmiokąta, w którym wszystkie kąty wewnętrzne są równe, zaś boki mają długości 1, 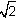 , 1,
, 1, 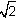 , 1,
, 1, 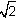 , 1,
, 1,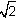 w podanej kolejności.
w podanej kolejności.
Rozwiązanie
Najpierw narysujmy odpowiedni rysunek do zadania.
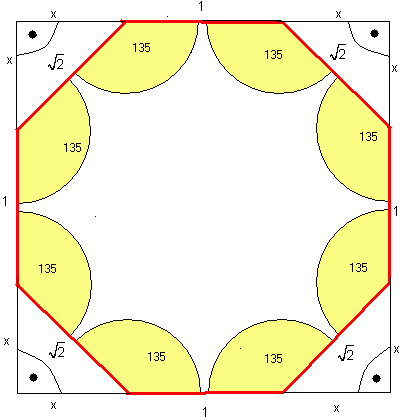
Zauważamy, iż trójkąty narożne na rysunku są prostokątne. Wobec tego możemy obliczyć x z Tw. Pitagorasa:
a2+b2=c2
Podstawiając dane do tego wzoru wyliczamy x:
x2+x2=(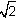 )2
)2
2x2=2
x="1
Mamy już wyliczone x, więc możemy zabrać się za obliczenie pola i obwodu figury.
POLE
Pole obliczymy odejmując pole kwadratu od pola czterech trójkątów narożnych.
Pk- pole kwadratu
Pt- pole trójkąta narożnego
Po- pole ośmiokąta
Pk-4Pt=Po
Po=32-4(1/2*1*1)=9-4*1/2="9-2=7
Po=7
OBWÓD
4*1+4*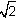 =4+4
=4+4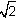
Odpowiedź
Pole tej figury wynosi 7, a obwód 4+4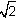
Bartosz Majewski
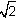 , 1,
, 1, 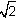 , 1,
, 1, 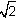 , 1,
, 1,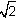 w podanej kolejności.
w podanej kolejności.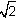 , 1,
, 1, 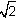 , 1,
, 1, 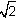 , 1,
, 1,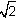 w podanej kolejności.
w podanej kolejności.