LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM
Zadanie 12
Wszystkie wierzchołki czworokąta ABCD leżą na okręgu,
przekątne czworokąta przecinają się w punkcie S różnym od środka okręgu.
Ile stopni ma kąt ACD jeśli |<DAB|=80°, |< BSC|=110°, |<ABC|=80°?
Rozwiązanie:
Przyjmijmy oznaczenie jak na rysunku:
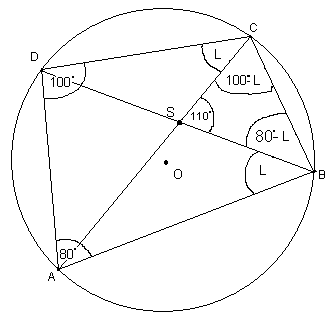
Wiemy, że sumy przeciwległych kątów w czworokącie dają 180°,
jeśli da się ten czworokąt wpisać w okrąg. Stąd kąty przy wierzchołkach D oraz C mają po 100°. Oznaczmy szukany kąt ACD przez L. Wówczas kąt ABD również ma miarę L, ponieważ są to kąty wpisane oparte na tym samym łuku. Rozpatrzmy trójkąt BCS. Kąt przy wierzchołku B mam miarę 80°-L, a kąt przy wierzchołku C mam miarę 100°-L. Suma kątów w trójkącie jest równa 180', zatem:
110° + (80°-L) + (100°-L) = 180°. Rozwiązując równanie z jedną niewiadomą otrzymujemy L="55°.
Odpowiedź:
Kąt ACD ma 55°.
Rozalia Makowska
