LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS I GIMNAZJUM
Zadanie 12
Wśród wszystkich prostokątów o obwodzie 100 cm wyznacz ten,
który ma największe pole. Odpowiedź uzasadnij.
Rozwiązanie:
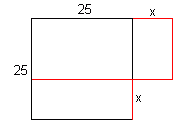
Prostokąty o tym samym obwodzie 100 cm, możemy tworzyć wydłużając dwa równoległe boki kwadratu 25×25 i wydłużając o tyle samo dwa pozostałe boki tego kwadratu.
 |
Ţ |
 |
Pokażę, że wśród tych prostokątów najwieksze pole ma kwadrat.
Oznaczam:
P = pole prostokąta
Pk = pole kwadratu
P = (25 + x)×(25 - x) = 25×25 - 25×x + 25×x - x2 = 252 - x2
P = 252 - x2
Pk = 252
x2 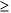 0
0
252 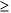 252 - x2
252 - x2
Pk 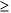 P.
P.
Odpowiedź:
Wśród wszystkich prostokątów o obwodzie 100 cm największe pole ma kwadrat o boku 25 cm.
Rozalia Makowska




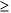 0
0 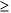 252 - x2
252 - x2
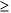 P.
P.