LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM
Zadanie 14
Zbiór liczb naturalnych {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} dzielimy na dwa niepuste i rozłączne podzbiory tak, by iloczyn elementów pierwszego podzbioru był podzielny przez iloczyn elementów drugiego podzbioru (na przykład, I = {1, 3, 4, 5, 7, 8, 9}, II = {2, 6, 10}). Dla każdego podziału obliczamy iloraz tych iloczynów. Jaką najmniejszą wartość może mieć taki iloraz?
Rozwiązanie:
Rozłóżmy liczby, będące elementami zbioru {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, na czynniki pierwsze:
1=1
2=2
3=3
4=2×2
5=5
6=2×3
7=7
8=2×2×2
9=3×3
10=2×5
Aby iloczyn elementów pierwszego zbioru był podzielny przez iloczyn elementów drugiego zbioru, ilość odpowiednich czynników pierwszych, tworzących liczby z pierwszego zbioru, musi być większa bądź równa od ilości czynników pierwszych z drugiego zbioru.
Na przykład dla zbiorów, których iloczyny wyglądają następująco:
a) Iloczyn pierwszego zbioru:
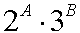
b) Iloczyn drugiego zbioru:
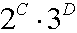
Aby zachodziła podzielność, musi być spełniony warunek:
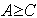
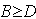
gdzie
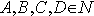
i oznaczają ilości odpowiednich czynników pierwszych.
W naszym przypadku iloraz ma być jak najmniejszy, zatem będziemy dążyć, aby ilości "dwójek", "trójek", "piątek" w obu zbiorach były równe. Po zliczeniu czynników pierszych otrzymaliśmy: 8 "dwójek", 4 "trójki", 2 "piątki" i 1 "siódemkę". Możliwe jest takie rozgrupowanie elementów zawierających dwójki, trójki i piątki, że iloczyn elementów jednego zbioru jest równy iloczynowi elementów drugiego zbioru. Kombinacją taką jest np. {2×5; 3×3; 2×2×2} i {2; 5; 2×3; 2×2}. Nie ma jednak wśród liczb "siódemki", która jest tylko jedna i nie możemy jej sparować z żadnym innym elementem. Należy umieścić ją w pierwszym zbiorze, aby podzielność była spełniona. Gdy w pierwszym zbiorze znajdzie się 7, iloraz iloczynów elementów zbiorów będzie równy 7:
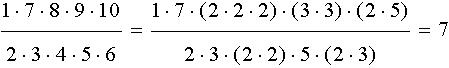
Odpowiedź:
Taki iloraz może mieć najmniejszą wartość równą 7.
Rozalia Makowska