LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM

Zadanie 13

1. pięciokąt wypukły, który ma wszystkie kąty rozwarte?
2. pięciokąt wypukły, w którym wszystkie kąty są ostre?
3. sześciokąt wypukły, w którym cztery kąty są ostre i dwa kąty są rozwarte?
4. sześciokąt wypukły, w którym cztery kąty są rozwarte i dwa kąty są ostre?

Rozwiązanie

Suma miar kątów pięciokąta jest równa 540° a w sześciokącie 720°.

1. Czy można narysować pięciokąt wypukły, który ma wszystkie kąty rozwarte?

   Tak, można. Może to być na przykład pieciokąt foremny:

   

   

   Każdy z pięciu kątów jest rozwarty.

2. Czy można narysować pięciokąt wypukły, w którym wszystkie kąty są ostre?
   

   Nie, gdyby wszystkie kąty były ostre ich miary byłyby mniejsze niż 90° co w sumie daje mniej niż 540°.
   

   

   Więc nie możemy go narysować.

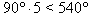
   Suma miar kątów pięciokąta jest równa 540°.

3. Czy można narysować sześciokąt wypukły, w którym cztery kąty są ostre i dwa kąty są rozwarte?

   Nie da się. Jeśli cztery kąty są ostre to suma ich miar jest mniejsza niż
   
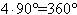
   Pozostałe dwa muszą być wypukłe więc suma ich miar jest mniejsza niż
   .
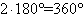   Ostatecznie suma kątów jest mniejsza niż suma kątów sześciokąta czyli 720°.

4. Czy można narysować sześciokąt wypukły, w którym cztery kąty są rozwarte i dwa kąty są ostre?

   Tak, jest to możliwe, ponieważ jeżeli cztery kąty sa rozwarte to suma ich miar jest mniejsza niż
   .
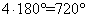   Pozostałe dwa kąty są ostre więc ich miara jest mniejsza niż
   .
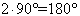   Suma miar jest mniejsza niż 900°, więc rysując kąty o odpowiedniej mierze uzyskamy 720°.
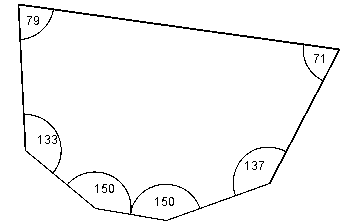
   np.
   

   

Mikołaj Niedziela