Rozwiązanie
- Ile soli należy wsypać do 12 kg wody, aby otrzymać czteroprocentową solankę?
- Ile wody należy dodać do 6 kg pięcioprocentowej solanki, aby otrzymać solankę dwuprocentową?
- Ile soli należy dosypać do 10 kg pięcioprocentowej solanki, aby otrzymać roztwór dwudziestoprocentowy? Naczynie po lewej stronie wypełnione jest roztworem wody i soli o masie 10kg. Woda w tym roztworze stanowi 95%, a sól (s) 5%.
Naczynie z wodą po lewej stronie jest wypełnione 12 kg soli. Woda w tym naczyniu stanowi 100%, (sól stanowi 0%).
Nastepnie do naczynia dodajemy sól(m) tak, by stanowiła 4% masy roztworu (sytuacje ilustruje naczynie po prawej). Masa wody się nie zmienia dodajemy tylko m soli. WAŻNE jest, by pamiętać, że sól stanowi 4% tego roztworu wody z sola, którego masa wynosi 12kg+m!!! Możemy zatem wyprowadzić równanie:
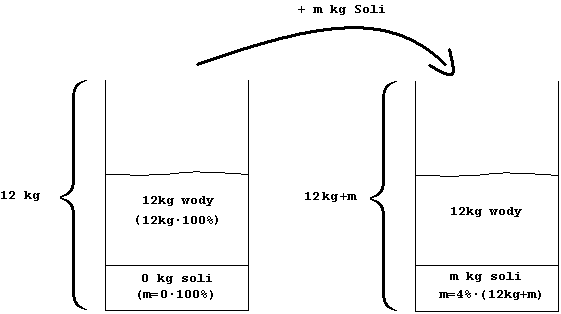
m="4%*(12kg+m)" / Mnożymy obie strony równania przez 100, żeby pozbyć się procentu.
100m="4*(12kg+m)" / Przekształcamy wzór tożsamościowo, pozbywając się nawiasu.
100m="48kg+4m" / Odejmujemy od obydwu stron równania 4m.
96m="48kg" / Dzielimy obydwie strony równania przez 96.
m="0,5kg."
Odpowiedź.
Należy dosypać 0,5 kg soli.W naczyniu po lewej stronie znajduje się 6kg roztworu wody i soli. Woda(w) w tym roztworze stanowi 95%, a sól 5%.
W naczyniu po prawej stronie znajduje się 6kg+w roztworu. Woda w tym roztworze stanowi 98%, a sól( której ilość się nie zmieniła w porównaniu z pierwszym naczyniem) stanowi 2% tego roztworu. Możemy więc wyprowadzić wzór:
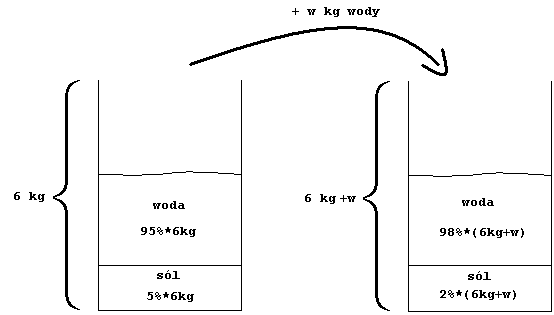
95%*6kg+w="98%*(6kg+w)" / Mnożymy obie strony równania przez 100, aby pozbyć się procentu.
95*6+100w="98*(6kg+w)" / Przekształcamy wzór tożsamościowo tak, by pozbyć się nawiasu.
570+100w="98*6kg+98w"
570+100w="588+98w" /Odejmujemy od obydwu stron 570.
100w="18+98w" / Odejmujemy od obydwu stron 98w.
2w="18" / Dzielimy obydwie strony równania przez 2.
w="9
Odpowiedź. Należy dolać 9litrów (kg) wody.
Naczynie po prawej stronie wypelnione jest roztworem o masie 10kg+s. Woda w tym roztworze stanowi 80%, a sól 20%. Ponieważ nie zmienia się ilość wody możemy wyprowadzić następujące rówanie:
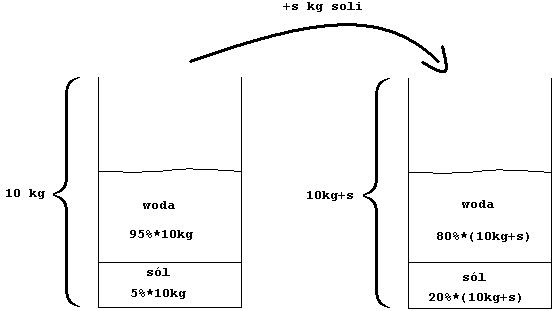
5%*10kg+s="20%*(10kg+s)" / Mnożymy obie strony równania przez 100, aby pozbyć się procentów.
5*10kg+100s="20*(10kg+s)" / Przekształcamy wzór tożsamościowo, aby pozbyć się nawiasu.
50kg+100s="200kg+20s" / Odejmujemy od obydwu stron 50kg.
100s="150kg+20s" / Odejmujemy od obydwu stron 20s.
80s="150kg" / Dzielimy obydwie strony równania przez 80.
s="1,875kg
Odpowiedź.
Należy dosypać 1,875kg soli.Mikołaj Niedziela