Udowadniam, że czworokąt OEBD jest prostokątem.
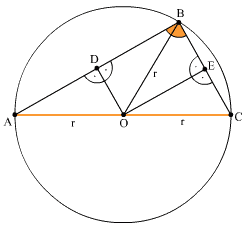Kąt przy wierzchołku B jest kątem wpisanym w okąg i opartym na średnicy więc musi być to kąt prosty.
Kąty przy wierzchołkach D i E są proste bo tak zostały narysowane odcinki OD i OE.
Czworokąt OEBD jest prostokątem ponieważ ma trzy kąty proste których suma jest równa 270°, więc na czwarty kąt przypada 90° stopni bo suma kątów w czworokącie jest równa 360°.
Uzasadniam, że |AD| = |DB| i |BE| = |EC|.
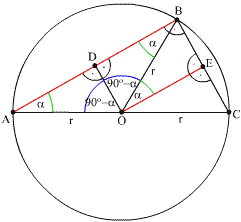Na rysunku zaznaczyłam równe kąty a naprzemianległe i odpowiadające, korzystając z tego, że odcinki OE i AB muszą być równoległe bo oba są prostopadłe do jednego odcinka BC.
Trójkąty AOD i BOD mają więc równe katy (90°, a, 90°-a) i wspólny bok OD.
Z cechy kbk przystawania trójkątów wynika, że trójkąt AOD przystaje do trójkąta BOD, więc |AD| = |DB|.
Podobnie możemy zauważyć, że trójkąty OCE i OBE są przystające, więc |BE| = |EC|.