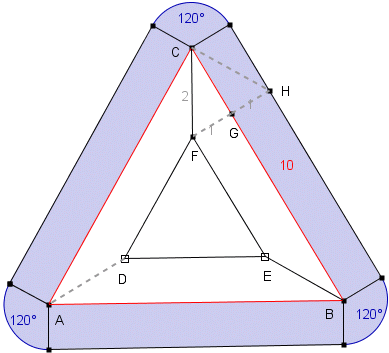
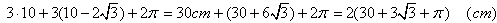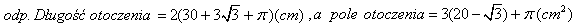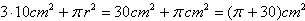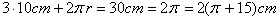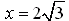LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM

Zadanie 17a

Brzeg trójkąta równobocznego o boku długości 10 cm "otoczono" zbiorem punktów, z których każdy jest odległy od jednego z boków o nie więcej niż 1 cm. Oblicz długość brzegu tego otoczenia i pole tego otoczenia.

Rozwiązanie

  1. POLE I OBWÓD OD ZEWNĄTRZ

    Otoczenia od zewnątrz
    = 3 prostokąty (o boku bokach 1 cm i 10 cm) + Koło (o promieniu r = 1 cm)

    Pz = Rozmiar: 486 bajtów

    Obwód otoczenia od strony zewnętrznej trójkąta:

    Obz = Rozmiar: 414 bajtów

  2. POLE I OTOCZENIE OD WEWNĄTRZ

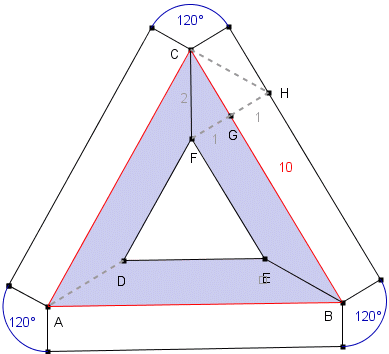
    Otoczenie od wewnątrz = 3 * pole trapezu BCFE

    Z twierdzenia Pitagorasa:

    x2 = 22 - 12
    x2 = 3

    Pole otoczenia od wewnątrz równa się: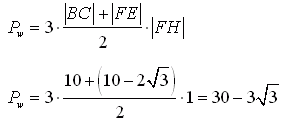

    Obwód otoczenia od strony wewnętrznej trójkąta: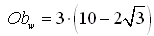

  3. POLE I OBWÓD CAŁOŚCI OTOCZENIA

    Łączne pole otoczenia

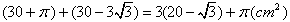
    Rozmiar: 501 bajtów

    Łączna długość otoczenia

    Rozmiar: 772 bajtów Rozmiar: 922 bajtów

rozwiązał Miłosz Paczkowski