LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM
Zad.17
Dany jest trójkąt równoramienny, w którym podstawa ma długość 24 cm, a ramię jest długości 15 cm. Obliczyć odległość między środkami okręgu wpisanego w ten trójkąt i okręgu opisanego na tym trójkącie.
Rozwiązanie
Sw - środek okręgu wpisanego w trójkąt ABC
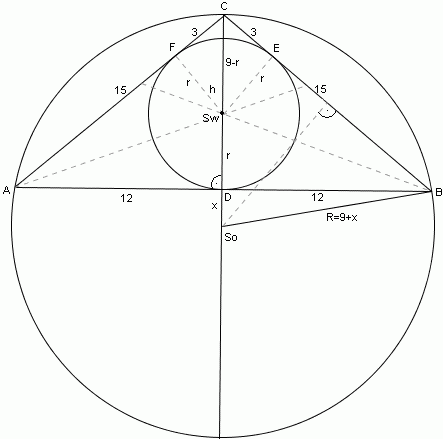
So - środek okręgu opisanego na trójkącie ABC
obliczyć : |SoSw| (odległość między środkami okręgów)
|SoSw| = r+x, r - promień okręgu wpisanego
h+x = R, R - promień okręgu opisanego
1.Obliczam h z trójkąta ADC(prostokątny).
|AD|=12cm
|AC|=15cm
|AD|=h
122+h2=152
144+h2=225
h2=81
h=9(cm)
|AD|=|DB|=|BE|=|AF|=12(cm)
|EC|=|FC|=15-12=3(cm) |
 |
2.Obliczam r z trójkąta CSw.
|CE|2+|ESw|2=|CSw|2
32+r2=(9-r)2
9+r2=81-18r+r2
18r=81-9
18r=72
r=4(cm)
3.Obliczam x z trójkąta SoDB(prostokątny).
R=h+x
R=9+x
|BD|2+x2=R2
122+x2=(9+x)2
144+x2=81+18x+x2
18x=63
x=3,5(cm)
odp.|SoSw|=r+x=4cm+3,5cm=7,5cm
rozwiązał Miłosz Paczkowski