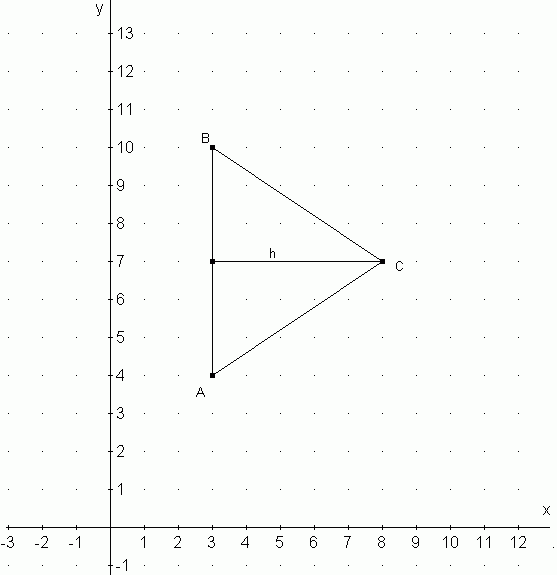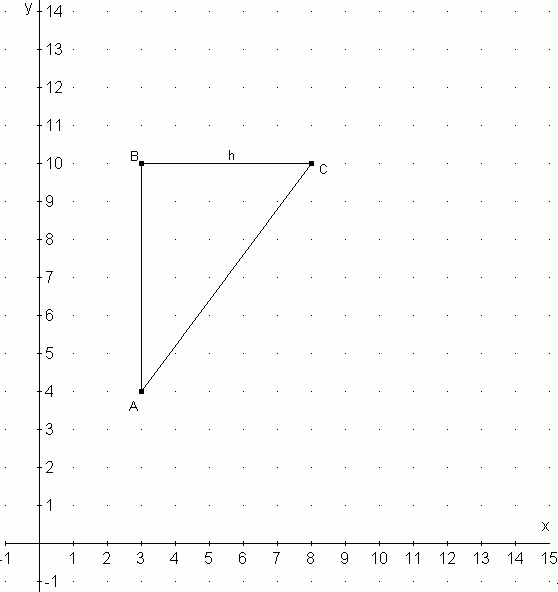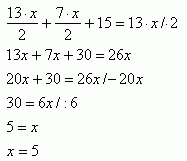LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS i GIMNAZJUMbr
Zadanie 17
Punkty A = (3,4) i B = (3,10) są wierzchołkami trójkąta ABC, którego pole jest równe 15. Znajdź współrzędne punktu C wiedząc, że:
a) trójkąt ABC jest równoramienny i odcinek AB jest jego podstawą,
b) trójkąt ABC jest prostokątny,
c) druga współrzędna punktu C jest równa -3.
Dane: A=(3,4) B=(3,10) C= ?
Rozwiązanie:
a)
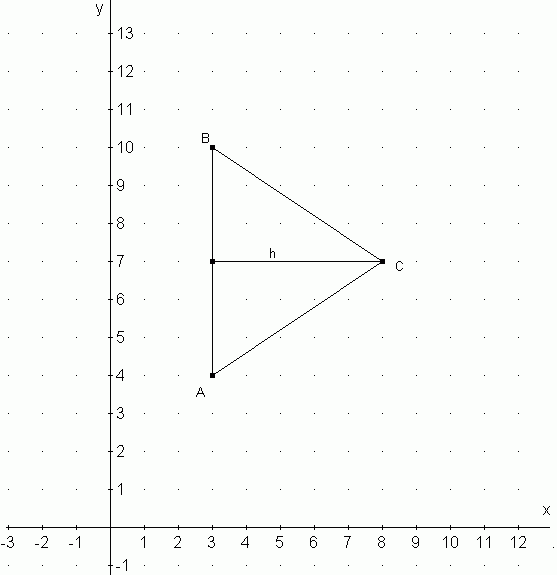
Z treści zadania wynika, że odcinek AB (o długości 6) jest podstawą trójkąta, którego pole wynosi 15, więc długość wysokości tego trójkąta musi wynieść pole trójkąta podzielone przez połowę podstawy, czyli 15:3, co równa się 5. Z danych wynika, że jest to trójkąt równoramienny, więc wysokość ta musi być wyprowadzona
z punktu dzielącego podstawę na połowy (tak jak na rysynku powyżej). Możliwości na rozwiązanie tego zadania są dwie - po 2 stronach podstawy, tzn. C=(8,7) lub C=(-2,7) (na rysunku pokazane jest tylko jedno rozwiązanie).
b)
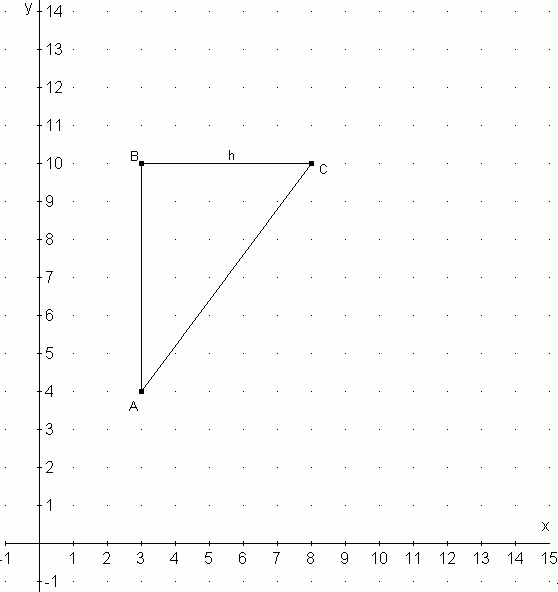
1) Jeżeli przyjęłoby się, że odcinek AB jest przyprostokątną tego trójkąta: wtedy długość jego wysokości jest taka sama jak w podpunkcie a), czyli 15:3. Jednak w tym przypadku z danych wynika, że ten trójkąt jest prostokątny, więc wysokość trzeba wyprowadzić od punktu A lub od punktu B. Jeśli więc przyjęłoby się, że odcinek AB jest przyprostokątną, to możliwości na rozwiązanie zadania są 4 - od punktu A w obie strony przyprostokątnej i od punktu B w obie strony przyprostokątnej, tzn. C=(8,10) lub C=(8,4) lub C=(-2,10 ) lub C=(-2,4) ( na rysunku powyżej przedstawione jest tylko jedno rozwiązanie).
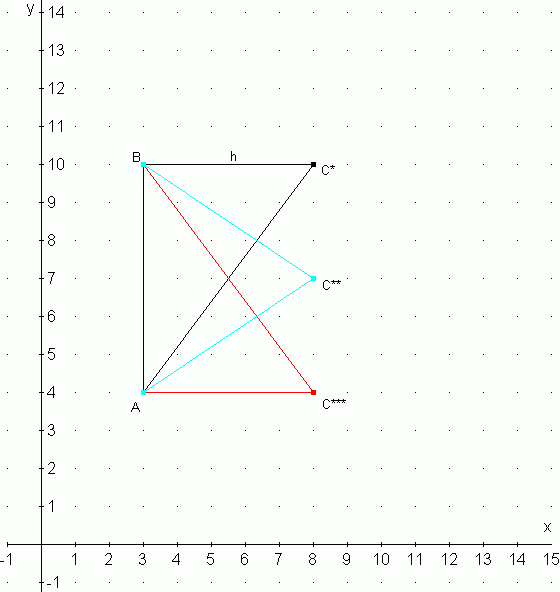
2)Jeżeli przyjęłoby się, że odcinek AB jest przeciwprostokątną trójkąta: kąty AC*B i AC***B są to kąty skrajne (proste). Jeżeli trzeba stworzyć trójkąt prostokątny, gdzie AB jest przeciwprostokątną, to kąt ACB musi być prosty. Jeżeli zmniejszałoby się współrzędną y punktu C, to miara kąta ACB zmniejszałaby się, aż do punktu C**. Od tego miejsca miara kąta ACB zwiększałaby się. Dlatego nie da się utworzyć trójkąta prostokątnego, gdzie AB jest jego przeciwprostokątną.
c)
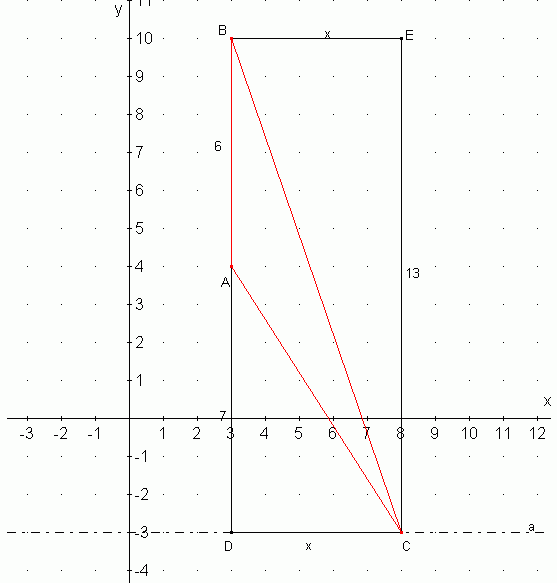
Z treści zadania wynika, że drugą współrzędną punktu C jest -3. Na początku trzeba zrobić rysunek pomocniczy. W związku z tym trzeba narysować prostą leżącą na współrzędnej -3 ( jest to prosta a), następnie stworzyć trójkąt ABC, gdzie C leży na prostej a. Potem należy obrysować ten trójkąt prosokątem (BDCE), tak, że punkty B i C są jego wierzchołkami. Odcinki DC i BE oznaczamy przez x. Znane jest teraz, że BA=6, AD=7, BD=13, DC=x, CE=13 i EB = x. Należy utworzyć równanie:
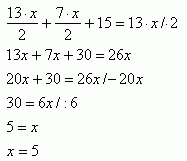
Jeżeli x=5, to istnieją 2 rozwiązania tego zadania - po dwóch stronach podstawy AB tzn. C=(8,-3) lub
C=(-2,-3) (na rysunku przedstawione jest tylko jedno rozwiązanie)
Maciej Perdenia kl. Ia