LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA NIESPODZIANKI
DLA KLAS I GIMNAZJUM
Zadanie 17
W 1990 r. - 1 lutego wypadł czwartek. W jaki dzień tygodnia wypadł tego samego roku prima aprilis?
Dane:
1990 r.
1 luty - czwartek
prima aprilis, czyli 1 kwietnia - ?
Rozwiązanie:
Na początku sprawdźmy, czy rok 1990 był rokiem przestępnym. Możemy to stwierdzić, sprawdzając, czy dany rok jest podzielny przez 4 ( rok jest przestępny gdy dzieli się przez 4 i nie dzieli się przez 400). Cecha podzielności przez 4 brzmi: "Jeśli 2 ostatnie cyfry danej liczby są podzielne przez 4, to ta liczba również jest podzielna przez 4." Sprawdźmy więc: 90:4="22" r. 2, co można określić wyrażeniem matematycznym: 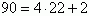 . Wiemy już, że rok 1990 nie był przestępny. Teraz musimy obliczyć, ile dni dzieli 1 kwietnia z 1 lutego. Luty ma w roku nieprzestępnym 28 dni, a marzec 31. Oznacza to, że prima aprilis z 1 lutego dzieli (28-1)+31+1 dni. Objaśnienie liczb:
. Wiemy już, że rok 1990 nie był przestępny. Teraz musimy obliczyć, ile dni dzieli 1 kwietnia z 1 lutego. Luty ma w roku nieprzestępnym 28 dni, a marzec 31. Oznacza to, że prima aprilis z 1 lutego dzieli (28-1)+31+1 dni. Objaśnienie liczb:
(28-1)->dni lutego - dzień opisany w zadaniu
31->dni marca
1->1 kwietnia
Po obliczeniu wyjdzie nam, że 1 kwietnia z 1 lutego dzieli 59 dni. Aby dowiedzieć się jakim dniem tygodnia jest 1 kwietnia należy podzielić 59 przez 7 (tydzień ma 7 dni). 59:7="8" r. 3, co można zapisać wyrażeniem matematycznym: 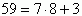 . Oznacza to, że 1 kwietnia to czwartek + 3 dni, czyli NIEDZIELA.
. Oznacza to, że 1 kwietnia to czwartek + 3 dni, czyli NIEDZIELA.
Odp. W 1990 roku prima aprilis wypadło w niedzielę.
Maciej Perdenia
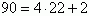 . Wiemy już, że rok 1990 nie był przestępny. Teraz musimy obliczyć, ile dni dzieli 1 kwietnia z 1 lutego. Luty ma w roku nieprzestępnym 28 dni, a marzec 31. Oznacza to, że prima aprilis z 1 lutego dzieli (28-1)+31+1 dni. Objaśnienie liczb:
. Wiemy już, że rok 1990 nie był przestępny. Teraz musimy obliczyć, ile dni dzieli 1 kwietnia z 1 lutego. Luty ma w roku nieprzestępnym 28 dni, a marzec 31. Oznacza to, że prima aprilis z 1 lutego dzieli (28-1)+31+1 dni. Objaśnienie liczb: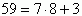 . Oznacza to, że 1 kwietnia to czwartek + 3 dni, czyli NIEDZIELA.
. Oznacza to, że 1 kwietnia to czwartek + 3 dni, czyli NIEDZIELA.