Uzasadnij, że w trójkącie prostokątnym suma długości przyprostokątnych jest równa sumie średnic okręgu wpisanego w ten trójkąt i okręgu opisanego na tym trójkącie.
Rozwiązanie:
Najpierw musimy konkstrukcyjnie przedstawić sytuację w zadaniu:
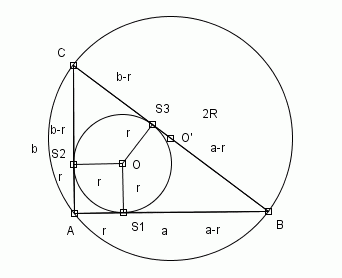
Oznaczenia:
A, B i C - wierzchołki trójkąta opisanego w zadaniu
a i b - przyprostokątne trójkąta ABC,
r - promień okręgu wpisanego w ten trójkąt,
R - promień okręgu opisanego na tym trójkącie,
S1, S2, S3 - punkty styczności boków trójkąta ABC z okręgiem w niego wpisanym,
O - środek okręgu wpisanego w ten trójkąt,
O'- środek okręgu opisanego na tym trójkącie,
Na początku prowadzimy promienie r do punktów styczności z trójkątem ABC. Powstaje kwadrat o boku r. Części boków a i b, które pozostały (S1B i S2C) możemy odpowiednio oznaczyć a-r i b-r. Korzystając z tego, że gdy poprowadzimy z dowolnego punktu 2 półproste styczne do okręgu, to odległości między tym punktem a punktami styczności z okręgiem są równe, możemy odcinek S3C oznaczyć jako b-r, a odcinek S3B jako a-r.
Na podstawie rysunku wyprowadzamy równanie:
(a-r)+(b-r)=2R
a+b-2r="2R" /+2r
a+b="2R+2r
(a+b) to suma długości przyprostokątnych trójkąta, a (2r+2R) to suma średnic okręgów opisanych w zadaniu, więc udowodniliśmy, co należało dowieść.
Maciej Perdenia