LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS VI SZKOŁY PODSTAWOWEJ
Zadanie 6
Uzasadnij, że równoległoboki ABCD i AEFG mają równe pola.
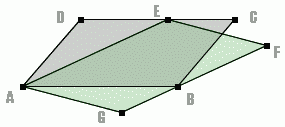
Rozwiązanie
Najpierw łączymy punkty E i B tak, by otrzymać trójkąt ABE.
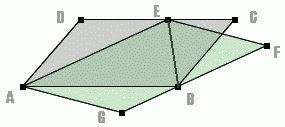
Jeżeli uznamy AB za podstawę trójkąta ABE, to jego wysokość będzie również wysokością równoległoboku ABCD.
Więc pole równoległoboku ABCD jest 2 razy większe niż pole trojkąta ABE.
Jeżeli uznamy AE za podstawę trójkąta ABE, to jego wysokość będzie również wysokością równoległoboku AEFG.
Więc pole równoległoboku AEFG jest 2 razy większe niż pole trojkąta ABE.
Stąd wiemy, że pola równoległoboków ABCD i AEFG są takie same, ponieważ oba równe są 2 razy tyle, ile pole trójkąta ABE.
Maciej Perdenia

