LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM
ZADANIE 18
Na okręgu o środku O oznaczono punkty A, B, C tak, że kąt ABC wpisany w ten okrąg ma miarę 40°, a kąt środkowy BOC ma miarę 160°. Oblicz miary kątów w trójkątach AOB, AOC, BOC.ROZWIĄZANIE
Trójkąt AOC
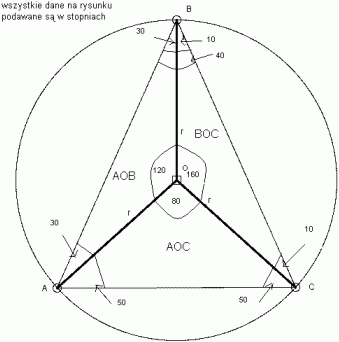 Kąt ABC, który ma 40° jest oparty na tym samym łuku co kąt AOC. Korzystając z twierdzenia, że kąt środkowy jest 2 razy większy od kąta wpisanego opartego na tym samymy łuku mamy, że kąt AOC ma 80°.
Kąt ABC, który ma 40° jest oparty na tym samym łuku co kąt AOC. Korzystając z twierdzenia, że kąt środkowy jest 2 razy większy od kąta wpisanego opartego na tym samymy łuku mamy, że kąt AOC ma 80°.Trójkąt AOB
Wiemy, że suma kątów środkowych w kole równa się 360°. Mamy podane już wartości kątów 80° i 160°, więc miara kąta AOB wynosi 360° - (80° + 160°) = 120°. Trójkąt AOB jest to również równoramienny: 180° - 120° = 60° i 60° : 2 = 30°, więc dwa pozostałe kąty tego trójkąta mają po 30°.Trójkąt BOC
Mamy podany tu już kąt 160°. Trójkat jest równoramienny więc możemy policzyć dwa pozsotałe kąty:ODPOWIEDZI znajdują się na rysunku.
Opracował
Jakub Polak