LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM
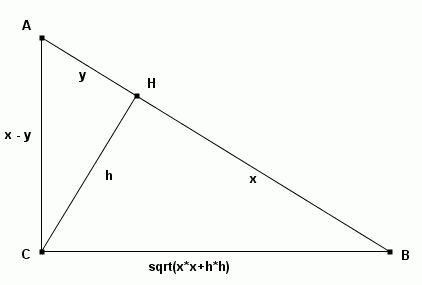
Wyznacz kąty trójkąta prostokątnego ABC, jeśli |BH| - |HA| = |AC|, gdzie odcinek CH jest wysokością opuszczoną z wierzchołka kąta prostego C.
Rozwiązanie|BH| - |HA| = |AC|
Odcinek |BH| oznaczamy jako x, odcinek |HA| oznaczamy jako y, a odcinek |AC|
oznaczamy jako x-y, h zaś oznacza wysokość CH. Z twierdzenia Pitagorasa dla trójkąta CBH bok BH ma długość pierwiastek z (x2 + h2).

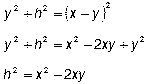
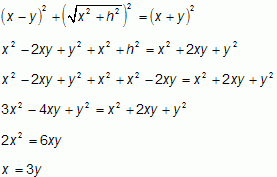
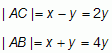
Odpowiedź
Kąty tego trójkąta to: 30o, 60o, 90o.
Opracował
Jakub Polak