LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS I GIMNAZJUM

Zadanie 21

Dla jakich wartości m , z odcinków 2m + 2, m + 8, 3m + 1 , można zbudować trójkąt równoramienny?

Rozwiązanie:

Najpierw przypomnijmy sobie co to jest trójkąt równoramienny:

Trójkąt równoramienny to trójkąt który ma 2 lub 3 boki tej samej długości. Boki, które mają tą samą miarę nazywamy ramionami, a pozostały bok podstawą.

Musimy jeszcze pamietać, że aby z odcinków mozna było stworzyć trójkąt musi być spełniona nierówność trójkąta czyli: suma długości dwóch krótszych odcinków musi być większa niż długość trzeciego odcinka.

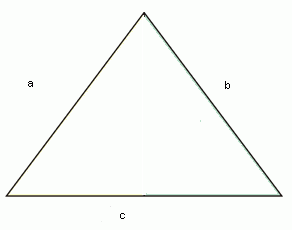
Niech a = 2m + 2, b = m + 8 i c = 3m + 1.

Rozważmy teraz 3 przypadki

Przypadek 1: a = b

a = b

2m + 2 = m + 8     / -m

m + 2 = 8     / -2

m = 6

a = 14

b = 14

c = 19

Sprawdzenie:

14 + 14 = 28

28 > 19

Można ułożyć taki trójkąt

Przypadek 2: a = c

a = c

2m + 2 = 3m + 1     /  -2m

2 = m + 1     / -1

1 = m

m = 1

a = 4

b = 9

c = 4

Sprawdzenie:

4 + 4 = 8

8 < 9

Nie można ułożyć takego trójkąta

Przypadek 3: b = c

b = c

m + 8 = 3m + 1      / -m

8 = 2m + 1      /-1

7 = 2m       /:2

3,5 = m

m = 3,5

a = 9

b = 11,5

c = 11,5

Sprawdzenie:

11,5 + 11,5 = 23

23 > 9

Można ułożyć taki trójkąt

Odpowiedź:

Karol Romanowski kl Ia